题目内容
3.已知α为锐角,当$\frac{2}{1-tanα}$无意义时,tan(α+15°)-tan(α-15°)的值是$\frac{2\sqrt{3}}{3}$.分析 根据特殊角的三角函数值和分式有意义的条件求解.
解答 解:当$\frac{2}{1-tanα}$无意义时,tanα=1,
∠α=45°,
则tan(α+15°)-tan(α-15°)=tan60°-tan30°=$\sqrt{3}$-$\frac{\sqrt{3}}{3}$
=$\frac{2\sqrt{3}}{3}$.
故答案为:$\frac{2\sqrt{3}}{3}$.
点评 本题考查了特殊角的三角函数值,解答本题的关键是掌握几个特殊角的三角函数值以及分式有意义的条件.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.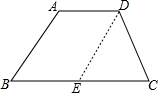 如图,将梯形ABCD的腰AB沿AD平移,平移长度等于AD的长,则下列说法不正确的是( )
如图,将梯形ABCD的腰AB沿AD平移,平移长度等于AD的长,则下列说法不正确的是( )
 如图,将梯形ABCD的腰AB沿AD平移,平移长度等于AD的长,则下列说法不正确的是( )
如图,将梯形ABCD的腰AB沿AD平移,平移长度等于AD的长,则下列说法不正确的是( )| A. | AB∥DE且AB=DE | B. | ∠DEC=∠B | C. | AD∥EC且AD=EC | D. | BC=AD+EC |
12.某校七年级1、2两班组织班会活动,两班生活委员分别到集市上购买苹果,苹果的价格如下表:
1班分两次共购买苹果70千克(第二次多于第一次),共付出189元,而2班则一次购苹果70千克.
(1)2班比1班少付多少元?
(2)1班第一次、第二次分别购买苹果多少千克?
| 购买苹果数 | 不超过30千克 | 30千克以上但不超过50千克 | 50千克以上 |
| 每千克价格 | 3元 | 2.5元 | 2元 |
(1)2班比1班少付多少元?
(2)1班第一次、第二次分别购买苹果多少千克?
 如图,四边形ABCD内接于⊙O,∠C=110°,连接OB、OD,则∠BOD=140°.
如图,四边形ABCD内接于⊙O,∠C=110°,连接OB、OD,则∠BOD=140°. 如图所示,直线AB,CD相交于点O,若∠1-∠2=60°,则∠1=140°,∠2=40°.
如图所示,直线AB,CD相交于点O,若∠1-∠2=60°,则∠1=140°,∠2=40°.