题目内容
16.不等式组$\left\{\begin{array}{l}{x-2>0}\\{\frac{x}{2}≤4}\end{array}\right.$的解集是( )| A. | x≥8 | B. | x>2 | C. | 0<x<2 | D. | 2<x≤8 |
分析 先求出两个不等式的解集,再求其公共解.
解答 解:$\left\{\begin{array}{l}{x-2>0①}\\{\frac{x}{2}≤4②}\end{array}\right.$,
解不等式①得:x>2.
解不等式②得:x≤8.
所以,原不等式组的解集为2<x≤8.
故选:D.
点评 本题主要考查了一元一次不等式组解集的求法,其简便求法就是用口诀求解.求不等式组解集的口诀:同大取大,同小取小,大小小大中间找,大大小小找不到(无解).

练习册系列答案
相关题目
1.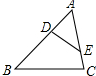 如图所示,D,E分别在△ABC的边AB、AC上,DE与BC不平行,当满足∠ADE=∠C或∠AED=∠B或$\frac{AD}{AC}$=$\frac{AE}{AB}$条件时,有△ABC∽△AED.
如图所示,D,E分别在△ABC的边AB、AC上,DE与BC不平行,当满足∠ADE=∠C或∠AED=∠B或$\frac{AD}{AC}$=$\frac{AE}{AB}$条件时,有△ABC∽△AED.
 如图所示,D,E分别在△ABC的边AB、AC上,DE与BC不平行,当满足∠ADE=∠C或∠AED=∠B或$\frac{AD}{AC}$=$\frac{AE}{AB}$条件时,有△ABC∽△AED.
如图所示,D,E分别在△ABC的边AB、AC上,DE与BC不平行,当满足∠ADE=∠C或∠AED=∠B或$\frac{AD}{AC}$=$\frac{AE}{AB}$条件时,有△ABC∽△AED.
8.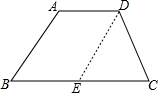 如图,将梯形ABCD的腰AB沿AD平移,平移长度等于AD的长,则下列说法不正确的是( )
如图,将梯形ABCD的腰AB沿AD平移,平移长度等于AD的长,则下列说法不正确的是( )
 如图,将梯形ABCD的腰AB沿AD平移,平移长度等于AD的长,则下列说法不正确的是( )
如图,将梯形ABCD的腰AB沿AD平移,平移长度等于AD的长,则下列说法不正确的是( )| A. | AB∥DE且AB=DE | B. | ∠DEC=∠B | C. | AD∥EC且AD=EC | D. | BC=AD+EC |
 如图,四边形ABCD内接于⊙O,∠C=110°,连接OB、OD,则∠BOD=140°.
如图,四边形ABCD内接于⊙O,∠C=110°,连接OB、OD,则∠BOD=140°. 如图所示,已知平行四边形ABCD和平行四边形EBFD的顶点A、E、F、C在一条直线上,求证:AE=CF.
如图所示,已知平行四边形ABCD和平行四边形EBFD的顶点A、E、F、C在一条直线上,求证:AE=CF.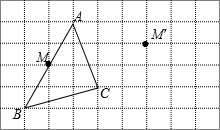 (1)如图,点M是△ABC中AB的中点,经平移后,点M落在M′处.请在正方形网格中画出△ABC平移后的图形△A′B′C′.
(1)如图,点M是△ABC中AB的中点,经平移后,点M落在M′处.请在正方形网格中画出△ABC平移后的图形△A′B′C′.