题目内容
13. 如图,已知:∠A=∠1,∠2+∠3=180°,∠BDE=70°,
如图,已知:∠A=∠1,∠2+∠3=180°,∠BDE=70°,(1)AB与DF平行吗?说明理由;
(2)求∠ACB的度数.
分析 (1)根据已知条件得到∠BEC=∠3,由平行线的判定定理即可得到结论.
(2)由平行线的性质得到∠BED=∠1,等量代换得到∠BED=∠A,推出DE∥AC,根据平行线的性质即可得到结论.
解答 解:(1)AB与DF平行,
理由:∵∠2+∠BEC=180°,
∵∠2+∠3=180°,
∴∠BEC=∠3,
∴AB∥DF;
(2)∵AB∥DF,
∴∠BED=∠1,
∵∠A=∠1,
∴∠BED=∠A,
∴DE∥AC,
∴∠ACB=∠BDE=70°.
点评 本题考查了平行线的性质和判定,熟练掌握平行线的判定和性质是解题的关键.

练习册系列答案
相关题目
2.下列说法正确的是( )
| A. | 1的平方根是1 | B. | 1的算术平方根是1 | ||
| C. | -2是2的算术平方根 | D. | -1的平方根是-1 |
3.若$\overrightarrow{AB}$是非零向量,则下列等式正确的是( )
| A. | |$\overrightarrow{AB}$|=|$\overrightarrow{BA}$| | B. | |$\overrightarrow{AB}$|+|$\overrightarrow{BA}$|=0 | C. | $\overrightarrow{AB}$+$\overrightarrow{BA}$=0 | D. | $\overrightarrow{AB}$=$\overrightarrow{BA}$ |
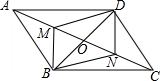 如图,在平行四边形ABCD中,M、N分别是OA,OC的中点,O为对角线AC与BD的交点,试问四边形BMDN是平行四边形吗?说说你的理由.
如图,在平行四边形ABCD中,M、N分别是OA,OC的中点,O为对角线AC与BD的交点,试问四边形BMDN是平行四边形吗?说说你的理由. 如图,在平行四边形ABCD中,对角线AC、BD相交于点O,若E、F是AC上的两个动点,分别从A、C两点以相同的速度向C、A运动,其速度为2cm/s.
如图,在平行四边形ABCD中,对角线AC、BD相交于点O,若E、F是AC上的两个动点,分别从A、C两点以相同的速度向C、A运动,其速度为2cm/s. 如图,已知BE=CF,AB∥CD,AB=CD. 求证:△ABF≌△DCE.
如图,已知BE=CF,AB∥CD,AB=CD. 求证:△ABF≌△DCE.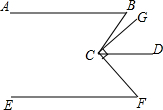 如图,已知AB∥CD,GC⊥CF,∠ABC=65°,CD是∠GCF的角平分线,∠EFC=40°.
如图,已知AB∥CD,GC⊥CF,∠ABC=65°,CD是∠GCF的角平分线,∠EFC=40°.