Question

1．已知菱形ABCD中，AC=6cm，BD=4cm．若以BD为边作正方形BDEF，则AF=$\sqrt{5}$或$\sqrt{53}$cm．

Answer 1

分析 作出图形，根据菱形的对角线互相垂直平分求出AO、BO，然后分正方形在A、C的两边两种情况延长CA（或AC）交EF于点M（或点N），根据勾股定理求出AF的长度即可得出结论．

解答 解：以BD为边作正方形BDEF分两种情况：
①如图1，正方形BDEF在点A一侧时，延长CA交EF于点M．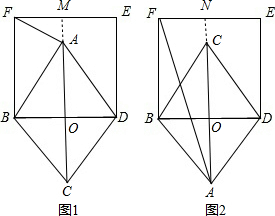
∵四边形ABCD为菱形，AC=6cm，BD=4cm，
∴OB=2cm，OA=3cm．
∵四边形BDEF为正方形，
∴FM=BO=2cm，AM=DE-OA=1cm，
∴AF=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$cm；
②如图2，正方形BDEF在点C一侧时，延长AC交EF于点N，
∵四边形ABCD为菱形，AC=6cm，BD=4cm，
∴OB=2cm，OA=3cm．
∵四边形BDEF为正方形，
∴FN=BO=2cm，AN=DE+OA=7cm，
∴AF=$\sqrt{{2}^{2}+{7}^{2}}$=$\sqrt{53}$cm．
故答案为：$\sqrt{5}$或$\sqrt{53}$．

点评 本题考查了菱形的性质，正方形的性质，勾股定理，主要利用了菱形的对角线互相垂直平分，难点在于分情况讨论并作辅助线构造出直角三角形，作出图形更形象直观．