题目内容
8. 如图,在平行四边形ABCD中,对角线AC、BD相交于点O,若E、F是AC上的两个动点,分别从A、C两点以相同的速度向C、A运动,其速度为2cm/s.
如图,在平行四边形ABCD中,对角线AC、BD相交于点O,若E、F是AC上的两个动点,分别从A、C两点以相同的速度向C、A运动,其速度为2cm/s.(1)当E与F不重合时,四边形DEBF是平行四边形吗?说明理由.
(2)若BD=24cm,AC=32cm,当运动时间t为何值时,以D、E、B、F为顶点的四边形是矩形?说明理由.
分析 (1)根据平行四边形的性质得出OA=OC,OB=OD,求出BD、EF互相平分,根据平行四边形的判定得出即可;
(2)根据矩形的性质求出EF=24cm,OE=OF=12cm,OA=OC=16cm,即可得出答案.
解答 证明:(1)当E与F不重合时,四边形DEBF是平行四边形,理由如下:
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵E、F两动点分别以A、C两点以相同的速度向C、A运动,
∴AE=CF,
∴OA-AE=OC-OF,即OE=OF,
∴BD、EF互相平分,
∴四边形DEBF是平行四边形;
(2)解:∵四边形DEBF是平行四边形,
∴当BD=EF时 四边形DEBF是矩形,
∵BD=24cm,
∴EF=24cm,
∴OE=OF=12cm,
∵AC=32cm,
∴OA=OC=16cm,
∴AE=4cm或28cm,
∵E、F两边动点的速度都是2cm/s,
∴t=2s 或t=14s,
∴当运动时间t=2s或14s时,以D、E、B、F为顶点的四边形是矩形.
点评 本题考查了矩形的判定,平行四边形的性质和判定的应用,能熟记矩形和平行四边形的性质和判定是解此题的关键.

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
20.若方程组$\left\{\begin{array}{l}{x+y=☆}\\{2x+y=16}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=6}\\{y=□}\end{array}\right.$,则被“☆”、“□”遮住的两个数分别是( )
| A. | 10,3 | B. | 3,10 | C. | 4,10 | D. | 10,4 |
18.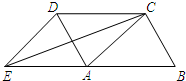 已知:如图,四边形ABCD是平行四边形,延长BA到点E,使AE=AB,联结ED、EC、AC.添加一个条件,能使四边形ACDE成为矩形的是( )
已知:如图,四边形ABCD是平行四边形,延长BA到点E,使AE=AB,联结ED、EC、AC.添加一个条件,能使四边形ACDE成为矩形的是( )
 已知:如图,四边形ABCD是平行四边形,延长BA到点E,使AE=AB,联结ED、EC、AC.添加一个条件,能使四边形ACDE成为矩形的是( )
已知:如图,四边形ABCD是平行四边形,延长BA到点E,使AE=AB,联结ED、EC、AC.添加一个条件,能使四边形ACDE成为矩形的是( )| A. | AC=CD | B. | AB=AD | C. | AD=AE | D. | BC=CE. |

 用尺规作一个角等于已知角的和,要求不写作法,但要保留作图痕迹;已知:∠1、∠2.求作:∠AOB,使∠AOB=∠1+∠2.
用尺规作一个角等于已知角的和,要求不写作法,但要保留作图痕迹;已知:∠1、∠2.求作:∠AOB,使∠AOB=∠1+∠2. 如图,已知:∠A=∠1,∠2+∠3=180°,∠BDE=70°,
如图,已知:∠A=∠1,∠2+∠3=180°,∠BDE=70°, 如图,在菱形ABCD中,AC=8,BD=6,DP⊥AB于点P,求PB.
如图,在菱形ABCD中,AC=8,BD=6,DP⊥AB于点P,求PB.