Question

5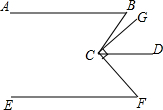．如图，已知AB∥CD，GC⊥CF，∠ABC=65°，CD是∠GCF的角平分线，∠EFC=40°．
①AB与EF平行吗？判断并说明理由．
②求∠BCG的度数．

Answer 1

分析 ①延长BC交EF于点M，根据平行线的性质和三角形的内角和即可得到结论；
②利用平行线的性质得出∠ABC=∠BCD=60°，∠DCF=∠EFC=45°，进而结合垂线的性质求出答案．

解答 解：①AB与EF不平行，
理由：延长BC交EF于点M，
∵AB∥CD，
∴∠BCD=∠B=65°，
∵GC⊥CF，
∴∠GCF=90°，
∵CD是∠GCF的角平分线，
∴∠GCD=45°，
∴∠BDG=20°，
∴∠MCF=70°，
∵∠F=40°，
∴∠CMF=70°，
∴∠ABC≠∠CMF
∴AB与EF不平行；
②∵AB∥CD，
∴∠BCD=∠ABC=65°，
∴∠BCG=∠BCD-∠GCD
=65°-45°
=20°．

点评 此题主要考查了平行线的性质，角平分线的定义，垂直的定义，正确掌握平行线的性质是解题关键．