题目内容
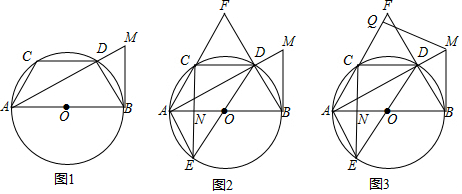
13.已知AB为⊙O的直径,CD为⊙O的弦,CD∥AB,过点B的切线与射线AD交于点M,连接AC、BD.(1)如图l,求证:AC=BD;
(2)如图2,延长AC、BD交于点F,作直径DE,连接AE、CE,CE与AB交于点N,求证:∠AFB=2∠AEN;
(3)如图3,在(2)的条件下,过点M作MQ⊥AF于点Q,若MQ:QC=3:2,NE=2,求QF的长.
分析 (1)连接OC,OD,根据平行线 的性质得到∠DAB=∠ADC根据已知条件得到∠COA=∠DOB,于是得到结论;
(2)连接OC,推出△FBA是等腰三角形,由DE是⊙O的直径,得到∠ECD=90°,根据平行线的性质得到AB⊥CE,得到AC=AE,根据等腰三角形的性质得到∠CAN=∠EAN=∠ABF,∠ACE=∠AEN,根据三角形的内角和即可得到结论;
(3)解:连接BC交AD于P,根据圆周角定理得到∠PAB=∠PBA,求得PA=PB,推出P为AM的中点,根据平行线的判定定理得到BC∥MQ,于是得到$\frac{AP}{PM}$=$\frac{AC}{QC}$,求得AC=CQ,设DF=3k,AD=4k,由勾股定理得,AF=5k=BF,求得BD=2k,根据平行线的性质得到∠EAN=∠ABD,求得tan∠EAN=2,即可得到结论.
解答  (1)证明:连接OC,OD,
(1)证明:连接OC,OD,
∵CD∥AB,
∴∠DAB=∠ADC,
∵∠DOB=2∠DAB,∠COA=2∠CDA,
∴∠COA=∠DOB,
∴AC=BD;
(2)连接OC,
∵∠COA=∠DOB,OA=OB=OC=OD,
∴∠CAB=∠DBA,
∴△FBA是等腰三角形,
∵DE是⊙O的直径,
∴∠ECD=90°,
∵CD∥AB,
∴∠ANC=90°,
∴AB⊥CE,
∴AC=AE,
∴∠CAN=∠EAN=∠ABF,∠ACE=∠AEN,
∵∠FAB+∠FBA+∠F=180°,∠CAE+∠AEC+∠ACE=180°,
∴∠F=∠ACE+∠AEC,
∴∠AFB=2∠AEN;
(3)解:连接BC交AD于P,
∵AC=BD,
∴$\widehat{AC}$=$\widehat{BD}$,
∴∠PAB=∠PBA,
∴PA=PB,∠PBM=∠PMB,
∴PB=PM,
∴P为AM的中点,
∵MQ⊥AF,BC⊥AF,
∴BC∥MQ,
∴$\frac{AP}{PM}$=$\frac{AC}{QC}$,
∴AC=CQ,
∵$\frac{MQ}{QC}$=$\frac{3}{2}$,
∴$\frac{MQ}{AQ}$=$\frac{3}{4}$,
∴tan∠MAQ=$\frac{3}{4}$,
∴tan∠F=$\frac{4}{3}$,
设DF=3k,AD=4k,由勾股定理得,AF=5k=BF,
∴BD=2k,
∴tan∠ABD=2,
∴DE为直径,
∴∠EAD=90=∠BDM,
∴AE∥BD,
∴∠EAN=∠ABD,
∴tan∠EAN=2,
∵NE=2,
∴AN=1,CN=2,
∴BN=4,AE=BD=$\sqrt{5}$,
∴DF=$\frac{3\sqrt{5}}{2}$,AC=BD=$\sqrt{5}$=CQ,
∴QF=$\frac{\sqrt{5}}{2}$
点评 本题考查了平行线的性质,圆周角定理,勾股定理,三角函数的定义,等腰三角形的判定和性质,平行线分线段成比例定理,正确的作出辅助线是解题的关键.

 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案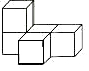 如图所示的几何体是由五个完全相同且棱长为1的正方体组成的,下列关于这个几何体的说法正确的是( )
如图所示的几何体是由五个完全相同且棱长为1的正方体组成的,下列关于这个几何体的说法正确的是( )| A. | 主视图的面积为5 | B. | 俯视图的面积为3 | ||
| C. | 左视图的面积为3 | D. | 三个视图的面积都为4 |
| A. | 5 | B. | 4 | C. | 3 | D. | 11 |
①一元二次方程ax2+4ax+m=0的两根为x1=-1,x2=-3
②原抛物线与y轴交于C点,CD∥x轴交抛物线于D点,则CD=4
③点E(1,y1),点F(-3,y2)在原抛物线上,则y2>y1
④抛物线y=ax2-4ax+m与原抛物线关于y轴对称.
其中正确的是( )
| A. | ①②③④ | B. | ①②④ | C. | ①② | D. | ①②③ |
| A. | -4 | B. | -1 | C. | 0 | D. | $\sqrt{2}$ |
| A. | -x5y3 | B. | -x6y | C. | x6y3 | D. | -x6y3 |
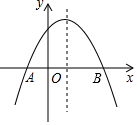 如图,抛物线y=ax2+bx+c,与x轴交于点A(-1,0),顶点坐标为(1,n),与y轴交点在(0,2)、(0,3)之间(包含端点),有下列结论:①abc>0;②4ac-b2>0;③当x=3时,y=0;④3a+b>0;⑤-1≤a≤-$\frac{2}{3}$,;⑥$\frac{8}{3}$≤n≤4,其中正确的有( )
如图,抛物线y=ax2+bx+c,与x轴交于点A(-1,0),顶点坐标为(1,n),与y轴交点在(0,2)、(0,3)之间(包含端点),有下列结论:①abc>0;②4ac-b2>0;③当x=3时,y=0;④3a+b>0;⑤-1≤a≤-$\frac{2}{3}$,;⑥$\frac{8}{3}$≤n≤4,其中正确的有( )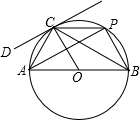 如图,点C是半径长为3的⊙O上任意一点,AB为直径,AC=3,过点C作⊙O的切线DC,点P为⊙O优弧AC上不与A、C重合的一个动点,点P从点C出发以每秒π个单位的速度顺时针匀速运动,到达点A停止运动.
如图,点C是半径长为3的⊙O上任意一点,AB为直径,AC=3,过点C作⊙O的切线DC,点P为⊙O优弧AC上不与A、C重合的一个动点,点P从点C出发以每秒π个单位的速度顺时针匀速运动,到达点A停止运动.