题目内容
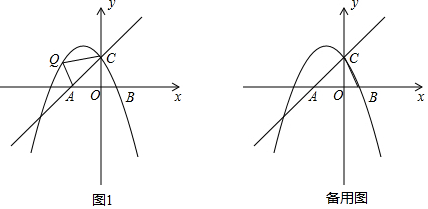
18.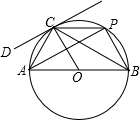 如图,点C是半径长为3的⊙O上任意一点,AB为直径,AC=3,过点C作⊙O的切线DC,点P为⊙O优弧AC上不与A、C重合的一个动点,点P从点C出发以每秒π个单位的速度顺时针匀速运动,到达点A停止运动.
如图,点C是半径长为3的⊙O上任意一点,AB为直径,AC=3,过点C作⊙O的切线DC,点P为⊙O优弧AC上不与A、C重合的一个动点,点P从点C出发以每秒π个单位的速度顺时针匀速运动,到达点A停止运动.(1)求∠DCA的度数;
(2)填空;
①当t=1s时,四边形OBPC是菱形;
②当t=3s时,由点A、P、C三点构成的三角形与△ABC全等.
分析 (1)根据切线的性质得到∠OCD=90°,根据等边三角形的性质即可得到结论;
(2)①当t=1s时,四边形OBPC是菱形;连接OP,根据弧长公式得到∠COP=60°,得到∠BOP=60°,推出△COP与△BOP是等边三角形,得到PC=PB=OB=OC,于是得到结论;
②当t=3s时,由点A、P、C三点构成的三角形与△ABC全等,根据弧长公式得到∠COP=180°,推出C,O,P三点共线,得到CP=AB,∠P′=∠B,根据全等三角形的判定即可得到结论.
解答  解:(1)∵CD是⊙O的切线,
解:(1)∵CD是⊙O的切线,
∴∠OCD=90°,
∵AC=OA=OC=3,
∴∠ACO=60°,
∴∠DCA=30°;
(2)①当t=1s时,四边形OBPC是菱形;
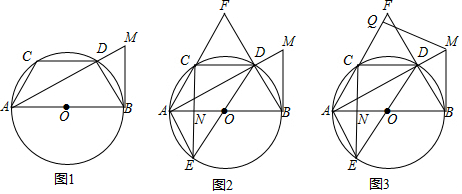
如图,1,连接OP,
∵t=1s,
∴$\widehat{PC}$的长度=π,
设∠POC=α,
∴$\frac{α•π×3}{180}$=π,
∴α=60°,
∴∠COP=60°,
∴∠BOP=60°,
∴△COP与△BOP是等边三角形,
∴PC=OC=OP=PB,
∴PC=PB=OB=OC,
∴四边形OBPC是菱形;
②当t=3s时,由点A、P、C三点构成的三角形与△ABC全等,
∵t=3s,
设∠COP=α,
∴$\widehat{CP}$的长=$\frac{α•π×3}{180}$=3π,
∴α=180°,
∴C,O,P三点共线,如图2,
∴CP=AB,∠P′=∠B,
在△ABC与△CP′A中,$\left\{\begin{array}{l}{∠ACB=∠CAP′}\\{∠B=∠P′}\\{AB=CP′}\end{array}\right.$,
∴△ABC≌△CP′A.
故答案为:1,3.
点评 本题考查了全等三角形的判定和性质,菱形的判定,等边三角形的判定和性质,切线的性质,正确理解题意是解题的关键.

 互动英语系列答案
互动英语系列答案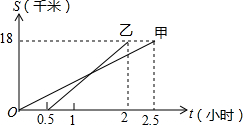 甲、乙两同学从A地出发,骑自行车在同一条路上行驶到距A地18千米的B地,他们离开A地的距离S(千米)和行驶时间t(小时)之间的函数关系图象如图所示,根据题目和图象所提供的信息,下列说法正确的是( )
甲、乙两同学从A地出发,骑自行车在同一条路上行驶到距A地18千米的B地,他们离开A地的距离S(千米)和行驶时间t(小时)之间的函数关系图象如图所示,根据题目和图象所提供的信息,下列说法正确的是( )| A. | 乙比甲先到达B地 | B. | 乙在行驶过程中没有追上甲 | ||
| C. | 乙比甲早出发半小时 | D. | 甲的行驶速度比乙的行驶速度快 |
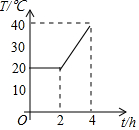 一个试验室在0:00-4:00的温度T(单位:℃)与时间t (单位:h)的函数关系的图象如图所示,在0:00-2:00保持恒温,在2:00-4:00匀速升温,则开始升温后试验室每小时升高的温度为( )
一个试验室在0:00-4:00的温度T(单位:℃)与时间t (单位:h)的函数关系的图象如图所示,在0:00-2:00保持恒温,在2:00-4:00匀速升温,则开始升温后试验室每小时升高的温度为( )| A. | 5℃ | B. | 10℃ | C. | 20℃ | D. | 40℃ |
| A. | a3+a2=2a5 | B. | 2a(1-a)=2a-2a2 | C. | (-ab2)3=a3b6 | D. | (a+b)2=a2+b2 |
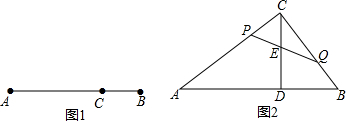
 如图,点A的坐标为(-8,0),点P的坐标为$({-\frac{7}{4},0})$,直线y=$\frac{3}{4}$x+b过点A,交y轴于点B,以点P为圆心,以PA为半径的圆交x轴于点C.
如图,点A的坐标为(-8,0),点P的坐标为$({-\frac{7}{4},0})$,直线y=$\frac{3}{4}$x+b过点A,交y轴于点B,以点P为圆心,以PA为半径的圆交x轴于点C.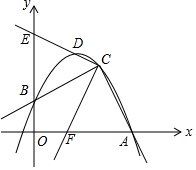 如图,已知二次函数y=ax2+bx+c的图象经过A(3,0),B(0,1),C(2,2)三点.
如图,已知二次函数y=ax2+bx+c的图象经过A(3,0),B(0,1),C(2,2)三点.