题目内容
4.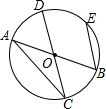 如图,AB和CD是⊙O的两条直径,弦BE∥CD,若∠BAC=30°,则$\frac{BE}{AB}$的值是( )
如图,AB和CD是⊙O的两条直径,弦BE∥CD,若∠BAC=30°,则$\frac{BE}{AB}$的值是( )| A. | $\frac{1}{2}$ | B. | 2 | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{3}$ |
分析 连接AE,根据等腰三角形的性质得到∠C=∠A=30°,由三角形的外角的性质得到∠BOC=60°,根据平行线的性质得到∠B=60°,根据三角函数的定义即可得到结论.
解答 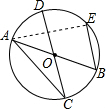 解:连接AE,
解:连接AE,
∵OA=OC,
∴∠C=∠A=30°,
∴∠BOC=60°,
∵BE∥CD,
∴∠B=∠BOC=60°,
∵AB是⊙O的直径,
∴∠AEB=90°,
∴$\frac{BE}{AB}$=cos∠B=$\frac{1}{2}$.故选A.
点评 本题考查了圆周角定理,平行线的性质,等腰三角形的性质,正确的识别图形是解题的关键.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
14. 如图,在?ABCD中,EF∥AB,点F为BD的中点,EF=4,则CD的长为( )
如图,在?ABCD中,EF∥AB,点F为BD的中点,EF=4,则CD的长为( )
 如图,在?ABCD中,EF∥AB,点F为BD的中点,EF=4,则CD的长为( )
如图,在?ABCD中,EF∥AB,点F为BD的中点,EF=4,则CD的长为( )| A. | $\frac{16}{3}$ | B. | 8 | C. | 10 | D. | 16 |
9.下列事件中,属必然事件的是( )
| A. | 掷一枚骰子,点数为3的一面朝上 | |
| B. | 在一副扑克牌中随意抽7张牌,其中有4张是Q | |
| C. | 从1、3、5、7四个数中,随意取两个数,这两个数之和为偶数 | |
| D. | 同时掷两枚骰子,这两枚骰子的点数相乘的积为40 |
 如图,在?ABCD中,DB=CD,∠C=80°,AE⊥BD于点E.试求∠DAE的度数.
如图,在?ABCD中,DB=CD,∠C=80°,AE⊥BD于点E.试求∠DAE的度数.