题目内容
14．已知点P（3m-6，n+3）在x轴上，且P点到原点的距离小于3，求n的值及m的取值范围．分析 根据点P（3m-6，n+3）在x轴上，得到n+3=0，求得n=-3，由P点到原点的距离小于3，得到不等式，于是得到结论．
解答 解：∵点P（3m-6，n+3）在x轴上，
∴n+3=0，
∴n=-3，
∵P点到原点的距离小于3，
∴|3m-6|＜3，
∴-3＜3m-6＜3，
∴m的取值范围是1＜m＜3．
点评 本题考查点的坐标的相关知识；用到的知识点为：在y轴上的点的横坐标为0；在y轴上的点到原点的距离为点的纵坐标的绝对值．
练习册系列答案
教材全解字词句篇系列答案
相关题目
4．
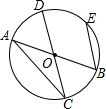如图，AB和CD是⊙O的两条直径，弦BE∥CD，若∠BAC=30°，则$\frac{BE}{AB}$的值是（ ）
如图，AB和CD是⊙O的两条直径，弦BE∥CD，若∠BAC=30°，则$\frac{BE}{AB}$的值是（ ）| A． | $\frac{1}{2}$ | B． | 2 | C． | $\frac{\sqrt{3}}{2}$ | D． | $\frac{\sqrt{3}}{3}$ |
5．关于x、y的方程组$\left\{\begin{array}{l}{x+2y=3m}\\{x-y=9m}\end{array}\right.$的解是方程3x+2y=17的一个解，那么m的值是（ ）
| A． | 2 | B． | -1 | C． | 1 | D． | -2 |
2．若点P（m+1，m+3）在x轴上，则点P的坐标为（ ）
| A． | （-2，0） | B． | （0，-2） | C． | （0，-4） | D． | （4，0） |
如图，在△ABC和△EDB中，∠C=∠EBD=90°，点E在AB上．若△ABC≌△EDB，AC=4，BC=3，则AE=1．
3．方程x-3=2x-4的解为（ ）
| A． | 1 | B． | -1 | C． | 7 | D． | -7 |