题目内容
16．
如图，在?ABCD中，DB=CD，∠C=80°，AE⊥BD于点E．试求∠DAE的度数．
分析 要求∠DAE，就要先求出∠ADB，要求出∠ADB，就要先求出∠DBC．利用DB=DC，∠C=80°即可求出．
解答 解：∵DB=DC，∠C=80°，
∴∠DBC=∠C=80°，
由AD∥BC，
∴∠ADE=∠DBC=80°，
∵AE⊥BD，
∴∠AEB=90°，
那么∠DAE=90°-∠ADE=10°
故∠DAE的度数为10°．
点评 本题考查了平行四边形的性质，解决本题的关键是利用三角形内角和定理，等边对等角等知识得到和所求角有关的角的度数．
练习册系列答案
相关题目
4．
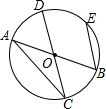如图，AB和CD是⊙O的两条直径，弦BE∥CD，若∠BAC=30°，则$\frac{BE}{AB}$的值是（ ）
如图，AB和CD是⊙O的两条直径，弦BE∥CD，若∠BAC=30°，则$\frac{BE}{AB}$的值是（ ）| A． | $\frac{1}{2}$ | B． | 2 | C． | $\frac{\sqrt{3}}{2}$ | D． | $\frac{\sqrt{3}}{3}$ |
11．若两个相似三角形的面积比为2：3，那么这两个三角形的周长的比为（ ）
| A． | 4：9 | B． | 2：3 | C． | $\sqrt{2}$：$\sqrt{3}$ | D． | 3：2 |
如图，在△ABC和△EDB中，∠C=∠EBD=90°，点E在AB上．若△ABC≌△EDB，AC=4，BC=3，则AE=1．