题目内容
14. 如图,在?ABCD中,EF∥AB,点F为BD的中点,EF=4,则CD的长为( )
如图,在?ABCD中,EF∥AB,点F为BD的中点,EF=4,则CD的长为( )| A. | $\frac{16}{3}$ | B. | 8 | C. | 10 | D. | 16 |
分析 首先根据三角形的中位线定理求出AB的长,然后根据平行四边形的性质求出CD的长.
解答 解:∵EF∥AB,点F为BD的中点,
∴EF是△ABD的中位线,
∵EF=4,
∴AB=8,
∵四边形ABCD是平行四边形,
∴CD=AB=8,
故选B.
点评 本题主要考查了平行四边形的性质以及三角形中位线定理的知识,解答本题的关键是根据三角形的中位线定理求出AB的长,此题难度不大.

练习册系列答案
相关题目
5.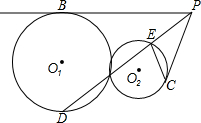 如图,⊙O1与⊙O2外切点A,半径为r1,r2,PB,PC分别为两圆的切线,B,C为切点,PB:PC=r1:r2,又PA交⊙O2于点E,则下面结论不正确的是( )
如图,⊙O1与⊙O2外切点A,半径为r1,r2,PB,PC分别为两圆的切线,B,C为切点,PB:PC=r1:r2,又PA交⊙O2于点E,则下面结论不正确的是( )
 如图,⊙O1与⊙O2外切点A,半径为r1,r2,PB,PC分别为两圆的切线,B,C为切点,PB:PC=r1:r2,又PA交⊙O2于点E,则下面结论不正确的是( )
如图,⊙O1与⊙O2外切点A,半径为r1,r2,PB,PC分别为两圆的切线,B,C为切点,PB:PC=r1:r2,又PA交⊙O2于点E,则下面结论不正确的是( )| A. | S△PAB:S△PCE=r12:r22 | B. | PA:PD=r2:r1 | ||
| C. | AE:AD=r2:r1 | D. | PB:PD=r2:r1 |
3.下列各组数中,能构成直角三角形的一组是( )
| A. | 4,5,6 | B. | 3,3,3$\sqrt{2}$ | C. | 6,8,11 | D. | 5,12,14 |
4.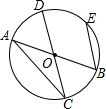 如图,AB和CD是⊙O的两条直径,弦BE∥CD,若∠BAC=30°,则$\frac{BE}{AB}$的值是( )
如图,AB和CD是⊙O的两条直径,弦BE∥CD,若∠BAC=30°,则$\frac{BE}{AB}$的值是( )
 如图,AB和CD是⊙O的两条直径,弦BE∥CD,若∠BAC=30°,则$\frac{BE}{AB}$的值是( )
如图,AB和CD是⊙O的两条直径,弦BE∥CD,若∠BAC=30°,则$\frac{BE}{AB}$的值是( )| A. | $\frac{1}{2}$ | B. | 2 | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{3}$ |
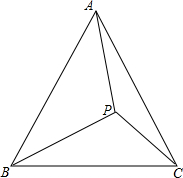 如图,在△ABC中,AB=BC,点P是△ABC内部的一点,∠BAP+∠BCP=90°,若AP=4,BP=5,CP=3,求证:△ABC为正三角形.
如图,在△ABC中,AB=BC,点P是△ABC内部的一点,∠BAP+∠BCP=90°,若AP=4,BP=5,CP=3,求证:△ABC为正三角形.