题目内容
19.已知a2mbn+6和3a3n-3b2m+n是同类项,则mn=27.分析 根据a2mbn+6和3a3n-3b2m+n是同类项,可以求得m、n的值,从而可解答本题.
解答 解:∵a2mbn+6和3a3n-3b2m+n是同类项,
∴$\left\{\begin{array}{l}{2m=3n-3}\\{n+6=2m+n}\end{array}\right.$
解得,$\left\{\begin{array}{l}{m=3}\\{n=3}\end{array}\right.$
∴mn=33=27,
故答案为:27.
点评 本题考查同类项,解题的关键是明确同类项的定义,会运用同类项的知识解答问题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.直角坐标系中,点P(x,y)在第三象限,且P到x轴和y轴的距离分别为3、7,则点P的坐标为( )
| A. | (-3,-7) | B. | (-7,-3) | C. | (3,7) | D. | (7,3) |
4.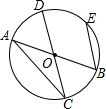 如图,AB和CD是⊙O的两条直径,弦BE∥CD,若∠BAC=30°,则$\frac{BE}{AB}$的值是( )
如图,AB和CD是⊙O的两条直径,弦BE∥CD,若∠BAC=30°,则$\frac{BE}{AB}$的值是( )
 如图,AB和CD是⊙O的两条直径,弦BE∥CD,若∠BAC=30°,则$\frac{BE}{AB}$的值是( )
如图,AB和CD是⊙O的两条直径,弦BE∥CD,若∠BAC=30°,则$\frac{BE}{AB}$的值是( )| A. | $\frac{1}{2}$ | B. | 2 | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{3}$ |
11.若两个相似三角形的面积比为2:3,那么这两个三角形的周长的比为( )
| A. | 4:9 | B. | 2:3 | C. | $\sqrt{2}$:$\sqrt{3}$ | D. | 3:2 |
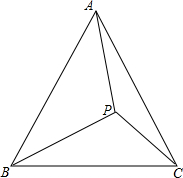 如图,在△ABC中,AB=BC,点P是△ABC内部的一点,∠BAP+∠BCP=90°,若AP=4,BP=5,CP=3,求证:△ABC为正三角形.
如图,在△ABC中,AB=BC,点P是△ABC内部的一点,∠BAP+∠BCP=90°,若AP=4,BP=5,CP=3,求证:△ABC为正三角形.