题目内容
12.已知关于x的四次三项式ax4-(a-12)x3-(b+3)x2-bx+11中不含x3及x2项,试写出这个多项式,并求x=-1时,这个多项式的值.分析 根据关于x的四次三项式ax4-(a-12)x3-(b+3)x2-bx+11中不含x3及x2项,可以求得a、b的值,从而可以写出这个单项式,进而可以求得x=-1时,这个多项式的值.
解答 解:∵关于x的四次三项式ax4-(a-12)x3-(b+3)x2-bx+11中不含x3及x2项,
∴$\left\{\begin{array}{l}{a-12=0}\\{b+3=0}\end{array}\right.$
解得,$\left\{\begin{array}{l}{a=12}\\{b=-3}\end{array}\right.$
∴四次三项式ax4-(a-12)x3-(b+3)x2-bx+11化简,得12x4+3x+11,
当x=-1时,12x4+3x+11=12×(-1)4+3×(-1)+11=12-3+11=20.
点评 本题考查多项式,解题的关键是明确多项式中如果不含某项,则这项的系数就是0.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
3.下列各组数中,能构成直角三角形的一组是( )
| A. | 4,5,6 | B. | 3,3,3$\sqrt{2}$ | C. | 6,8,11 | D. | 5,12,14 |
4.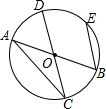 如图,AB和CD是⊙O的两条直径,弦BE∥CD,若∠BAC=30°,则$\frac{BE}{AB}$的值是( )
如图,AB和CD是⊙O的两条直径,弦BE∥CD,若∠BAC=30°,则$\frac{BE}{AB}$的值是( )
 如图,AB和CD是⊙O的两条直径,弦BE∥CD,若∠BAC=30°,则$\frac{BE}{AB}$的值是( )
如图,AB和CD是⊙O的两条直径,弦BE∥CD,若∠BAC=30°,则$\frac{BE}{AB}$的值是( )| A. | $\frac{1}{2}$ | B. | 2 | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{3}$ |
2.若点P(m+1,m+3)在x轴上,则点P的坐标为( )
| A. | (-2,0) | B. | (0,-2) | C. | (0,-4) | D. | (4,0) |