练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
不改变分式的值,把下列各式的分子与分母中各项的系数都化为整数.
① 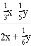 =__________; ②
=__________; ② 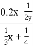 =____________;
=____________;
③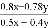 =___________; ④
=___________; ④ 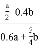 =____________.
=____________.
 【解析】① = ;
② =;
③= ;
④ = .
【解析】① = ;
② =;
③= ;
④ = . 过多边形的一个顶点的所有对角线把多边形分成8个三角形,这个多边形的边数是( )
A. 8 B. 9 C. 10 D. 11
 C
【解析】设多边形有n条边,
则n-2=8,解得n=10,
所以这个多边形的边数是10,
故选C.
C
【解析】设多边形有n条边,
则n-2=8,解得n=10,
所以这个多边形的边数是10,
故选C. 如图,?ABCD的周长为36,对角线AC、BD相交于点O,点E是CD的中点,BD=12,求△DOE的周长.
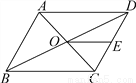
 △DOE的周长为15.
【解析】试题分析:根据平行四边形的对边相等和对角线互相平分可得,OB=OD,又因为E点是CD的中点,可得OE是△BCD的中位线,可得OE=BC,所以易求△DOE的周长.
试题解析:∵平行四边形ABCD的周长为36,
∴2(BC+CD)=36,则BC+CD=18.
∵四边形ABCD是平行四边形,对角线AC,BD相交于点O,BD=12,
∴OD=O...
△DOE的周长为15.
【解析】试题分析:根据平行四边形的对边相等和对角线互相平分可得,OB=OD,又因为E点是CD的中点,可得OE是△BCD的中位线,可得OE=BC,所以易求△DOE的周长.
试题解析:∵平行四边形ABCD的周长为36,
∴2(BC+CD)=36,则BC+CD=18.
∵四边形ABCD是平行四边形,对角线AC,BD相交于点O,BD=12,
∴OD=O... 比较下面每小题中两个算式结果的大小(在横线上填“>”、“<”或“=”).
⑴32+42 2×3×4;⑵22+22 2×2×2;⑶12+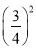 2×1×
2×1×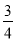 ;
;
⑷(-2) 2+52 2×(-2)×5;⑸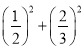
通过观察上面的算式,请你用字母来表示上面算式中反映的一般规律.
 (1)>(2)=(3)>(4)>(5)>; ≥2ab(当a=b时取等号).
【解析】试题分析:分别根据有理数的乘方法则求出各数的值,再根据有理数比较大小的法则比较出各数的大小,并总结出规律.
试题解析:(1)∵32+42=25,2×3×4=24,
∴32+42>2×3×4;
(2)∵22+22=8,2×2×2=8,
∴22+22=2×2×2;
(3)∵12+()...
(1)>(2)=(3)>(4)>(5)>; ≥2ab(当a=b时取等号).
【解析】试题分析:分别根据有理数的乘方法则求出各数的值,再根据有理数比较大小的法则比较出各数的大小,并总结出规律.
试题解析:(1)∵32+42=25,2×3×4=24,
∴32+42>2×3×4;
(2)∵22+22=8,2×2×2=8,
∴22+22=2×2×2;
(3)∵12+()... 若0<a<1,用“<”连接a,1, 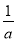 ,结果为___________________.
,结果为___________________.
 a<1<
【解析】∵0<a<1,
∴两边都除以a得,1<,
∴a<1<,
故答案为:a<1<.
a<1<
【解析】∵0<a<1,
∴两边都除以a得,1<,
∴a<1<,
故答案为:a<1<. a是非负数的表达式是( )
A. a>0 B.  ≥0 C. a≤0 D. a≥0
≥0 C. a≤0 D. a≥0
 D
【解析】非负数是指大于或等于0的数,所以a≥0,
故选D.
D
【解析】非负数是指大于或等于0的数,所以a≥0,
故选D. 在直线、线段、角、两条平行直线组成的图形、两条相交直线组成的图形这些图形中,是轴对称图形的有( )
A. 5个 B. 4个 C. 3个 D. 2个
 A
【解析】利用轴对称图形的定义对各图形进行判断即可得出结论.
【解析】
由轴对称的性质得,直线是轴对称图形,线段是有两条对称轴的轴对称图形,角的对称轴是其角平分线所在的直线;两条平行直线也是轴对称图形,两条相交直线也是轴对称图形,都是轴对称图形,故有5个.
故选A.
A
【解析】利用轴对称图形的定义对各图形进行判断即可得出结论.
【解析】
由轴对称的性质得,直线是轴对称图形,线段是有两条对称轴的轴对称图形,角的对称轴是其角平分线所在的直线;两条平行直线也是轴对称图形,两条相交直线也是轴对称图形,都是轴对称图形,故有5个.
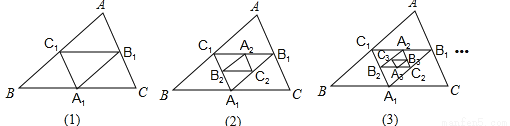
故选A. 如图,在图(1)中,A1、B1、C1分别是△ABC的边BC、CA、AB的中点,在图(2)中,A2、B2、C2分别是△A1B1C1的边B1C1、C1A1、A1B1的中点,…,按此规律,则第n个图形中平行四边形的个数共有_________个
 3n
【解析】略
因为每次增加一个三角形,就增加3个平行四边形,那么n次后,就有3n个平行四边形了
3n
【解析】略
因为每次增加一个三角形,就增加3个平行四边形,那么n次后,就有3n个平行四边形了 
