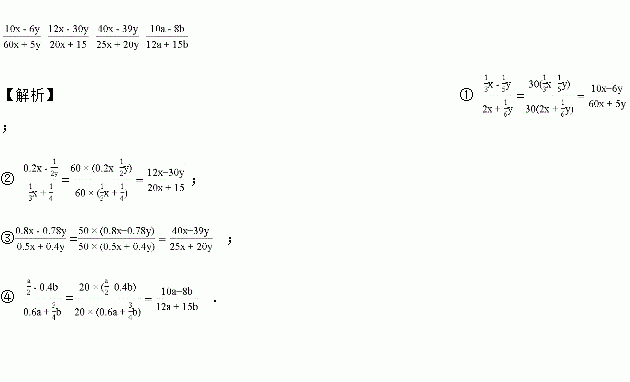题目内容
不改变分式的值，把下列各式的分子与分母中各项的系数都化为整数．
①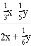 
=__________； ② 
=____________；
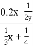③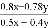
=___________； ④ 
=____________．
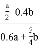【解析】① = ；
② =；
③= ；
④ = ．
练习册系列答案
新课标同步训练系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
多项式
的公因式是________.
【解析】提公因式法关键是如何找公因式．方法是：一看系数、二看字母（相同的字母或因式，次数最低），可得公因式为xy.
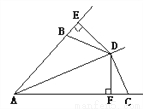
故答案为：xy. 如图所示，AD是∠BAC的平分线，DE⊥AB于E，DF⊥AC于F，且BD=CD，那么BE与CF相等吗？为什么？
见解析
【解析】试题分析：首先由角平分线的性质可得DE=DF，然后根据HL可证Rt△BDE≌Rt△CDF，即可证明BE=CF．
试题解析：相等.
理由是：∵AD平分∠BAC，DE⊥AB，DF⊥AC，
∴DE=DF,∠DEB=∠DFC=90°，
在Rt△BDE和Rt△CDF中，
，
∴Rt△BDE≌Rt△CDF(HL)，
∴BE=CF. 在下列说法中，正确的有（ ）个．
①三角对应相等的两个三角形全等；②三边对应相等的两个三角形全等；③两角，一边对应相等的两个三角形全等；④两边，一角对应相等的两个三角形全等.
A. 1 B. 2 C. 3 D. 4
B
【解析】①三角对应相等的两个三角形不一定全等，错误；
②三边对应相等的两个三角形全等，正确；
③两个角和其中一角的对边对应相等的两个三角形全等，正确；
④两条边和其中一边的对角对应相等的两个三角形不一定全等，错误；
故选：B 已知x2＋3x－1=0，求x－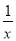
和x2＋
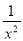的值．
－3,11
【解析】分析：首先将3x移项,再方程两边同除以x得出即可,再利用,方程两边同时平方求出即可.
本题解析：
因为 ,
所以 ,
将上式子两边同时除以x(x≠0),
所以 ,
,
,
则.故答案为：-3，,11. 化简分式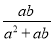
的结果为_____.
【解析】= ，故答案为： . 若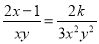
，则k的值为 （ ）
A. 3x2y2(2x-1) B. 
xy(2x-1) C. 
xy2(2x-1) D. xy2(2x-1)
B
【解析】∵, ∴2k=,∴k= (6x²y-3xy)= xy(2x-1).故选B. 已知一个多边形的内角和比它的外角和的3倍少180°，求这个多边形的边数．
7
【解析】试题分析：多边形的外角和是360°，根据多边形的内角和比它的外角和的3倍少180°，即可得到多边形的内角和的度数．根据多边形的内角和定理即可求得多边形的边数
试题解析：【解析】
设多边形的边数为n，依题意得
（n－2）．180°＝ 3×360°－180°
解得n＝7
答：这个多边形的边数是7