Question

18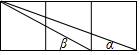．如图，在边长为1的正方形网格内连结不同的对角线得到∠α和∠β，则∠α+∠β=45度．

Answer 1

分析 取∠DBC=β，连接AC，根据勾股定理可求出AB、AC、BC的长度，根据三者间的关系利用勾股定理的逆定理即可得出△ABC为等腰直角三角形，根据等腰直角三角形的性质即可得出α+β的度数．

解答 解：取∠DBC=β，连接AC，如图所示．
∵AB=$\sqrt{{3}^{2}+{1}^{2}}$=$\sqrt{10}$，AC=BC=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$，
∴AC²+BC²=AB²，
∴△ABC为等腰直角三角形，
∴∠ABC=α+β=45°．
故答案为：45°．

点评 本题考查了勾股定理、勾股定理的逆定理以及等腰直角三角形，通过边与边的关系利用勾股定理的逆定理证出△ABC为等腰直角三角形是解题的关键．