题目内容
1. 如图,矩形ABCD中,点A在坐标原点,点B、点D分别在x轴、y轴的正半轴上,且AB=8,AD=6,
如图,矩形ABCD中,点A在坐标原点,点B、点D分别在x轴、y轴的正半轴上,且AB=8,AD=6,①请直接写出点C的坐标(8,6);
②点P从点D向C运动,速度为1个单位/秒,点Q从点B向A运动,速度点P相同,设运动时间为t秒,t为何值时C点在PQ的垂直平分线上,并求出此时P、Q的坐标.
分析 (1)根据图象可以直接到到点C的坐标;
(2)根据题意可以得到CP=CQ,从而可以得到t的值,以及此时P、Q的坐标.
解答 解:(1)∵在矩形ABCD中,点A在坐标原点,点B、点D分别在x轴、y轴的正半轴上,且AB=8,AD=6,
∴点C的坐标为(8,6),
故答案为:(8,6);
(2)由题意可得,
CP=CQ,
∴8-t=$\sqrt{{t}^{2}+{6}^{2}}$,
解得,t=$\frac{7}{4}$,
∴点P的坐标为($\frac{7}{4}$,6),点Q的坐标为($\frac{25}{4}$,0),
即当t=$\frac{7}{4}$秒时,C点在PQ的垂直平分线上,此时点P的坐标为($\frac{7}{4}$,6),点Q的坐标为($\frac{25}{4}$,0).
点评 本题考查矩形的性质、坐标与图形的性质、线段与垂直平分线的性质,解题的关键是明确题意,找出所求问题需要的条件.

练习册系列答案
相关题目
 如图,有长为24m的篱笆,一面利用墙(墙的最大长度a为13m),围成中间隔有一道篱笆的矩形花圃,设花圃的宽AB为x m,面积为Sm2.
如图,有长为24m的篱笆,一面利用墙(墙的最大长度a为13m),围成中间隔有一道篱笆的矩形花圃,设花圃的宽AB为x m,面积为Sm2. 如图:在直角坐标系中,O是坐标原点,已知A(4,3),P是坐标轴上的一点,若以O、A、P三点组成的三角形为等腰三角形,则满足条件的点P共有8个,写出其中一个点P的坐标是(5,0)(答案不唯一).
如图:在直角坐标系中,O是坐标原点,已知A(4,3),P是坐标轴上的一点,若以O、A、P三点组成的三角形为等腰三角形,则满足条件的点P共有8个,写出其中一个点P的坐标是(5,0)(答案不唯一). 如图,两圆相交于点P、Q,大圆的割线AD交小圆于点B、C,求证:∠APB+∠CQD=180°.
如图,两圆相交于点P、Q,大圆的割线AD交小圆于点B、C,求证:∠APB+∠CQD=180°. 如图,在△ABC中,∠BAC=120°,AB=AC,BC=12,AC的垂直平分线EF交AC于点E,交BC于点F,连接AF.
如图,在△ABC中,∠BAC=120°,AB=AC,BC=12,AC的垂直平分线EF交AC于点E,交BC于点F,连接AF.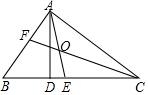 如图,在△ABC中,∠BAC=90°,∠B=50°,AE,CF是角平分线,它们相交于为O,AD是高,求∠BAD和∠AOC的度数.
如图,在△ABC中,∠BAC=90°,∠B=50°,AE,CF是角平分线,它们相交于为O,AD是高,求∠BAD和∠AOC的度数.