题目内容
6．一个多边形中，每个内角都相等，并且每个外角等于它的相邻内角的$\frac{2}{3}$，求这个多边形的外角．分析 首先设多边形内角为x°，则相邻的外角为$\frac{2}{3}$x°，根据题意可得方程x+$\frac{2}{3}$x=180，解出x的值，进而可得答案．
解答 解：设多边形内角为x°，
则x+$\frac{2}{3}$x=180，
解得：x=108，
外角为180°-108°=72°，
答：这个多边形的外角为72°．
点评 此题主要考查了多边形的内角与外角，关键是掌握多边形的内角与相邻的外角和为180°．
练习册系列答案
相关题目
如图，平面直角坐标系中，A（-4，0），B（0，4），过x轴正半轴上的点C作y轴的平行线，交直线AB于点D，P为直线CD上任意一点．作直线OP交直线AB于点Q，连接CQ．
14．
如图，以点O为圆心的两个同心圆中，大圆的弦AB是小圆的切线，点P是切点，AB=12$\sqrt{3}$，OP=6，则大圆的半径长为（ ）
如图，以点O为圆心的两个同心圆中，大圆的弦AB是小圆的切线，点P是切点，AB=12$\sqrt{3}$，OP=6，则大圆的半径长为（ ）| A． | 6 | B． | 6$\sqrt{3}$ | C． | 6$\sqrt{2}$ | D． | 12 |
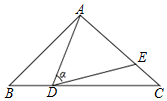如图，在△ABC中，AB=AC=10，BC=16，点D是边BC上一动点（不与B，C重合），∠ADE=∠B=α，DE交AC于点E，下列结论：
如图，矩形ABCD中，点A在坐标原点，点B、点D分别在x轴、y轴的正半轴上，且AB=8，AD=6，
8．
如图所示，在△ABC中，已知点D，E，F分别是BC，AD，CE的中点，S△ABC=4平方厘米，则S△BEF的值为（ ）
如图所示，在△ABC中，已知点D，E，F分别是BC，AD，CE的中点，S△ABC=4平方厘米，则S△BEF的值为（ ）| A． | 2平方厘米 | B． | 1平方厘米 | C． | $\frac{1}{2}$平方厘米 | D． | $\frac{1}{4}$平方厘米 |
如图，在平面直角坐标系中，