题目内容
15.甲与乙合作加工一批零件需要a天完成,若甲单独做需要b天完成,那么乙单独做需要多少天完成?分析 甲与乙合做的工作效率为$\frac{1}{a}$,甲的工作效率为$\frac{1}{b}$,所以乙的工作效率为$\frac{1}{a}$-$\frac{1}{b}$,然后用工作总量除以乙的工作效率即可得到乙单独做需要的天数.
解答 解:甲的工作效率为$\frac{1}{b}$,则乙的工作效率为$\frac{1}{a}$-$\frac{1}{b}$=$\frac{b-a}{ab}$,
所以乙单独做需要的时间=$\frac{1}{\frac{b-a}{ab}}$=$\frac{ab}{b-a}$(天).
点评 本题考查了列代数式(分式):把问题中与数量有关的词语,用含有数字、字母和运算符号的式子表示出来,就是列代数式. 本题的关键是表示出乙的工作效率.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.已知一次函数y=kx+b,当x的值增加2时,y值就增加4,则当x的值减少1时,y的值( )
| A. | 减少2 | B. | 减少4 | C. | 增加2 | D. | 增加4 |
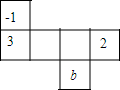 若x=1是方程$\frac{2a+x}{3}$-$\frac{x-bx}{6}$=1的解.
若x=1是方程$\frac{2a+x}{3}$-$\frac{x-bx}{6}$=1的解.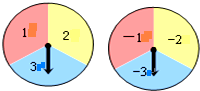 如图,有转盘A、B分别被分成三个面积相等的扇形,上面分别写有3个数字,用力转动两个转盘,转盘上的指针分别指向一个数字,则两个转盘指针指向的两个数之和恰好为0的概率是$\frac{1}{3}$.
如图,有转盘A、B分别被分成三个面积相等的扇形,上面分别写有3个数字,用力转动两个转盘,转盘上的指针分别指向一个数字,则两个转盘指针指向的两个数之和恰好为0的概率是$\frac{1}{3}$.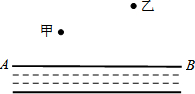 小河AB的同旁有甲、乙两个村庄,现计划在河岸AB上建一个水泵站,向两村供水,用以解决村民生活用水问题.若要求水泵站到甲、乙两村庄的距离相等,水泵站M应建在河岸AB上的何处?(要求:不写作法,但要保留作图痕迹,并写出作图结果)
小河AB的同旁有甲、乙两个村庄,现计划在河岸AB上建一个水泵站,向两村供水,用以解决村民生活用水问题.若要求水泵站到甲、乙两村庄的距离相等,水泵站M应建在河岸AB上的何处?(要求:不写作法,但要保留作图痕迹,并写出作图结果)