题目内容
7.化简下列各式:(1)$\frac{5xy}{20{y}^{2}}$;(2)$\frac{21{a}^{3}{b}^{4}c}{56{a}^{2}{b}^{5}d}$;(3)$\frac{x-y}{(y-x)^{3}}$;(4)$\frac{{x}^{2}-4{y}^{2}}{{x}^{2}-4xy+4{y}^{2}}$.分析 (1)分子分母约去公因式5y即可;
(2)分子分母约去公因式7a2b4即可;
(3)分子分母约去公因式(x-y)即可;
(4)先把分子分母因式分解,然后约去公因式(x-2y)即可.
解答 解::(1)$\frac{5xy}{20{y}^{2}}$=$\frac{x}{4y}$;
(2)$\frac{21{a}^{3}{b}^{4}c}{56{a}^{2}{b}^{5}d}$=$\frac{7{a}^{2}{b}^{4}•3ac}{7{a}^{2}{b}^{4}•8bd}$=$\frac{3ac}{8bd}$;
(3)$\frac{x-y}{(y-x)^{3}}$=-$\frac{x-y}{(x-y)^{3}}$=-$\frac{1}{(x-y)^{2}}$;
(4)$\frac{{x}^{2}-4{y}^{2}}{{x}^{2}-4xy+4{y}^{2}}$=$\frac{(x+2y)(x-2y)}{(x-2y)^{2}}$=$\frac{x+2y}{x-2y}$.
点评 本题考查了约分:约去分式的分子与分母的公因式,不改变分式的值,这样的分式变形叫做分式的约分.本题的关键是找出分子分母的公因式.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.已知a+b=$\sqrt{5}$,则$\frac{{a}^{2}-{a}^{2}{b}^{2}+{b}^{2}+2ab}{a+ab+b}$+ab等于( )
| A. | $\sqrt{5}$ | B. | $\frac{\sqrt{5}}{2}$ | C. | 2 | D. | 2$\sqrt{5}$ |
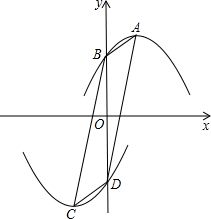 如图,抛物线l1:y=-x2+2bx+c(b>0)的顶点为A,与y轴交于点B;若抛物线l2与l1关于原点O成中心对称,其顶点为C,与y轴交于点D;其中点A、B、C、D中的任意三点都不在同一条直线上.
如图,抛物线l1:y=-x2+2bx+c(b>0)的顶点为A,与y轴交于点B;若抛物线l2与l1关于原点O成中心对称,其顶点为C,与y轴交于点D;其中点A、B、C、D中的任意三点都不在同一条直线上.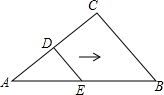 如图,D、E分别是AC和AB上的点,AD=DC=4,DE=3,DE∥BC,∠C=90°,将△ADE沿着AB边向右平移,当点D落在BC上时,平移的距离为5.
如图,D、E分别是AC和AB上的点,AD=DC=4,DE=3,DE∥BC,∠C=90°,将△ADE沿着AB边向右平移,当点D落在BC上时,平移的距离为5.