题目内容
3.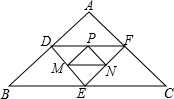 如图,点D、E、F分别是△ABC中AB、BC、AC边上的中点,点M、N、P分别是DE、EF、DF的中点.若△ABC的周长为24,则△PMN的周长为( )
如图,点D、E、F分别是△ABC中AB、BC、AC边上的中点,点M、N、P分别是DE、EF、DF的中点.若△ABC的周长为24,则△PMN的周长为( )| A. | 6 | B. | 8 | C. | 10 | D. | 12 |
分析 根据三角形中位线定理易得所求的三角形的各边长为原三角形各边长的一半,那么所求的三角形的周长就等于原三角形周长的一半求解即可.
解答 解:∵点D、E、F分别是AB、AC、BC的中点,
∴DE=$\frac{1}{2}$BC,EF=$\frac{1}{2}$AB,DF=$\frac{1}{2}$AC,
∴△DEF的周长=$\frac{1}{2}$(AB+BC+AC)=$\frac{1}{2}$×24=12,
同理可得:△PMN的周长=$\frac{1}{2}$×△DEF的周长6.
故选A.
点评 此题考查的是三角形中位线的性质,即三角形的中位线平行于第三边且等于第三边的一半.

练习册系列答案
相关题目
18.已知多项式x2-2kx+25是完全平方式,则k的值为( )
| A. | 5 | B. | -5 | C. | ±10 | D. | ±5 |
8.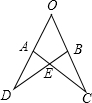 如图,OA=OB,OC=OD,∠O=50°,∠D=35°,则∠OAC等于( )
如图,OA=OB,OC=OD,∠O=50°,∠D=35°,则∠OAC等于( )
 如图,OA=OB,OC=OD,∠O=50°,∠D=35°,则∠OAC等于( )
如图,OA=OB,OC=OD,∠O=50°,∠D=35°,则∠OAC等于( )| A. | 65° | B. | 95° | C. | 45° | D. | 100° |
 如图,AB∥CD,E、F分别在AB、CD上,若∠1+∠D=180°,那么EF与BD平行吗?为什么?
如图,AB∥CD,E、F分别在AB、CD上,若∠1+∠D=180°,那么EF与BD平行吗?为什么?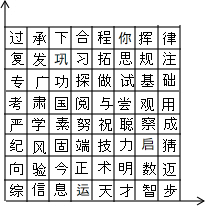 如图是一组密码的一部分,为了保密,许多情况下课采用不同的密码,请你运用所学知识找到破译的“钥匙”.目前,已破译出“正做数学”的真实意思是“祝你成功”.若“正”所处的位置为(x,y),你找到的密码钥匙是对应文字横坐标加1,纵坐标加2,破译的“今天考试”真实意思是“努力发挥”.
如图是一组密码的一部分,为了保密,许多情况下课采用不同的密码,请你运用所学知识找到破译的“钥匙”.目前,已破译出“正做数学”的真实意思是“祝你成功”.若“正”所处的位置为(x,y),你找到的密码钥匙是对应文字横坐标加1,纵坐标加2,破译的“今天考试”真实意思是“努力发挥”.