题目内容
12．在平面直角坐标系中，将抛物线y=x2-x-6向上（下）或向左（右）平移m个单位，使平移后的抛物线恰好经过原点，则m的最小值为2．分析 计算出函数与x轴、y轴的交点，将图象适当运动，即可判断出抛物线移动的距离及方向．
解答 
解：如图，当x=0时，y=-6，故函数图象与y轴交于点C（0，-6），
当y=0时，x2-x-6=0，即（x+2）（x-3）=0，
解得x=-2或x=3，
即A（-2，0），B（3，0）；
由图可知，函数图象至少向右平移2个单位恰好过原点，
故m的最小值为2．
故答案为2．
点评 本题考查了二次函数与几何变换，画出函数图象是解题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
2．如果一元二次方程x2+12x+27=0的两个根是x1，x2，那么x1+x2的值为（ ）
| A． | -6 | B． | -12 | C． | 12 | D． | 27 |
3．在Rt△ABC中，∠C=90°，下列等式中不成立的是（ ）
| A． | a=bcotB | B． | a=csinA | C． | $c=\frac{b}{cosA}$ | D． | acosB=c |
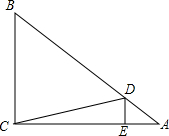如图，在Rt△ABC中，∠ACB=90°，$sinA=\frac{2}{3}$，点D、E分别在AB、AC上，DE⊥AC，垂足为点E，DE=2，DB=9，求
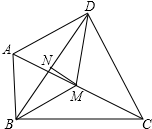如图，在四边形ABCD中，∠ABC=∠ADC=90°，M、N分别是AC、BD的中点，求证：
4．比-$\frac{1}{2}$的相反数小1的数是（ ）
| A． | $\frac{1}{2}$ | B． | -$\frac{1}{2}$ | C． | -1$\frac{1}{2}$ | D． | 1$\frac{1}{2}$ |
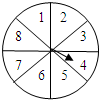如图所示，转盘被等分成8个扇形，并在上面依次标有数字1，2，3，4，5，6，7，8．（当指针指向边缘处，要重新转动到非边缘处）