题目内容
1.如图,已知数轴上点A表示的数为6,B是数轴上在A左侧的一点,且A,B两点间的距离为10.动点P从点A出发,以每秒6个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒.(1)数轴上点B表示的数是-4,点P表示的数是6-6t(用含t的代数式表示);
(2)动点Q从点B出发,以每秒4个单位长度的速度沿数轴向左匀速运动,若点P、Q时出发.求:
①当点P运动多少秒时,点P与点Q相遇?
②当点P运动多少秒时,点P与点Q间的距离为8个单位长度?

分析 (1)由已知得OA=6,则OB=AB-OA=4,因为点B在原点左边,从而写出数轴上点B所表示的数;动点P从点A出发,运动时间为t(t>0)秒,所以运动的单位长度为6t,因为沿数轴向左匀速运动,所以点P所表示的数是6-6t;
(2)①点P运动t秒时追上点Q,由于点P要多运动10个单位才能追上点Q,则6t=10+4t,然后解方程得到t=5;
②分两种情况:当点P运动a秒时,不超过Q,则10+4a-6a=8;超过Q,则10+4a+8=6a;由此求得答案解即可.
解答 解:(1)∵数轴上点A表示的数为6,
∴OA=6,
则OB=AB-OA=4,
点B在原点左边,
∴数轴上点B所表示的数为-4;
点P运动t秒的长度为6t,
∵动点P从点A出发,以每秒6个单位长度的速度沿数轴向左匀速运动,
∴P所表示的数为:6-6t;
(2)①点P运动t秒时追上点R,
根据题意得6t=10+4t,
解得t=5,
答:当点P运动5秒时,点P与点Q相遇;
②设当点P运动a秒时,点P与点Q间的距离为8个单位长度,
当P不超过Q,则10+4a-6a=8,解得a=1;
当P超过Q,则10+4a+8=6a,解得a=9;
答:当点P运动1或9秒时,点P与点Q间的距离为8个单位长度.
点评 此题考查的知识点是两点间的距离及数轴,根据已知得出各线段之间的关系等量关系是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.下列各题中,能用平方差公式计算的是( )
| A. | (a-$\frac{1}{2}$b)(a-$\frac{1}{2}$b) | B. | (a-$\frac{1}{2}$b)(-a+$\frac{1}{2}$b) | C. | (a-$\frac{1}{2}$b)(-a-$\frac{1}{2}$b) | D. | (a+$\frac{1}{2}$b)(-a-$\frac{1}{2}$b) |
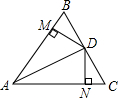 如图所示,△ABC中,AD平分∠BAC,点D是BC的中点,DM⊥AB,DN⊥AC,垂足分别为M,N,求证:∠B=∠C,BM=CN.
如图所示,△ABC中,AD平分∠BAC,点D是BC的中点,DM⊥AB,DN⊥AC,垂足分别为M,N,求证:∠B=∠C,BM=CN.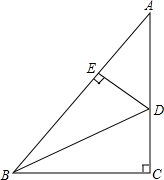 如图,Rt△ABC中,∠C=90°,BD是∠ABC的平分线,DE⊥AB于点E,AB=40cm,BC=24cm,S△ABC=384cm2,则DE的长是12cm.
如图,Rt△ABC中,∠C=90°,BD是∠ABC的平分线,DE⊥AB于点E,AB=40cm,BC=24cm,S△ABC=384cm2,则DE的长是12cm. 有理数a、b、c在数轴上的位置如图所示,化简|a+b|+|b+c|+|c+a|的结果是2a-2b-2c.
有理数a、b、c在数轴上的位置如图所示,化简|a+b|+|b+c|+|c+a|的结果是2a-2b-2c.