题目内容
2.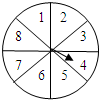 如图所示,转盘被等分成8个扇形,并在上面依次标有数字1,2,3,4,5,6,7,8.(当指针指向边缘处,要重新转动到非边缘处)
如图所示,转盘被等分成8个扇形,并在上面依次标有数字1,2,3,4,5,6,7,8.(当指针指向边缘处,要重新转动到非边缘处)(1)自由转动轮盘,当它停止转动时,指针指向的数字恰好能被3整除的概率是多少?
(2)请你利用这个转盘设计一个游戏,当自由转动转盘停止时,指针所指的区域的概率为$\frac{3}{4}$.
分析 (1)根据恰好能被3整除的数在整个圆盘中所占的份数即可解答;
(2)根据几何概率的意义,只需是满足条件的区域有6个即可,如当自由转动转盘停止时,指针指向区域的数小于7的概率(答案不唯一).
解答 解:(1)根据题意分析可得:转盘被等分成八个扇形,并在上面依次标有数字1,2,3,4,5,6,7,8;
恰好能被3整除的有2个,故自由转动转盘,当它停止转动时,指针指向的数恰好能被3整除的概率是$\frac{2}{8}$=$\frac{1}{4}$;
(2)根据随机事件概率的求法:当自由转动的转盘停止时,指针指向的区域的概率为$\frac{3}{4}$,只需是满足条件的区域有6个即可;如当自由转动转盘停止时,指针指向区域的数小于7的概率(答案不唯一).
点评 本题考查随机事件概率的求法与运用,一般方法为:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=$\frac{m}{n}$.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案
相关题目
10.下列各题中,能用平方差公式计算的是( )
| A. | (a-$\frac{1}{2}$b)(a-$\frac{1}{2}$b) | B. | (a-$\frac{1}{2}$b)(-a+$\frac{1}{2}$b) | C. | (a-$\frac{1}{2}$b)(-a-$\frac{1}{2}$b) | D. | (a+$\frac{1}{2}$b)(-a-$\frac{1}{2}$b) |
7.若关于x的方程ax2-4x-1=0是一元二次方程,则a满足的条件是( )
| A. | a>0 | B. | a≠0 | C. | a<0 | D. | a≠4 |
12.计算:36÷4×(-$\frac{1}{4}$)=( )
| A. | -36 | B. | $2\frac{1}{4}$ | C. | 36 | D. | $-\frac{9}{4}$ |
 有理数a、b、c在数轴上的位置如图所示,化简|a+b|+|b+c|+|c+a|的结果是2a-2b-2c.
有理数a、b、c在数轴上的位置如图所示,化简|a+b|+|b+c|+|c+a|的结果是2a-2b-2c. 如图,在△ABC中,AB=AC,AB的垂直平分线MN交AC于D,若AC=7cm,BC=3cm,则△DBC的周长是10cm.
如图,在△ABC中,AB=AC,AB的垂直平分线MN交AC于D,若AC=7cm,BC=3cm,则△DBC的周长是10cm.