题目内容
7.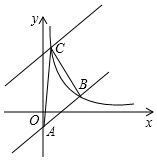 如图,在平面直角坐标系xOy中,直线y=x-2与y轴相交于点A,与反比例函数在第一象限内的图象相交于点B(m,2)
如图,在平面直角坐标系xOy中,直线y=x-2与y轴相交于点A,与反比例函数在第一象限内的图象相交于点B(m,2)(1)求该反比例函数关系式
(2)将直线y=x-2向上平移后与反比例函数在第一象限内的图象相交于点C,且△ABC的面积为18,求平移后的直线的解析式.
分析 (1)设反比例解析式为y=$\frac{k}{x}$,将B坐标代入直线y=x-2中求出m的值,确定出B坐标,将B的坐标代入反比例解析式中求出k的值,即可确定出反比例解析式;
(2)设平移后的直线交y轴于H,根据两平行线间的距离相等,可得C到AB的距离与H到AB的距离相等,根据等底等高的三角形的面积相等,可得b的值,根据待定系数法,可得答案.
解答 解:(1)设反比例解析式为y=$\frac{k}{x}$.
将B(m,2)代入直线y=x-2中得:m-2=2,
解得:m=4,
则B(4,2),
将B(4,2)代入y=$\frac{k}{x}$,得k=4×2=8, 则反比例解析式为y=$\frac{8}{x}$;
则反比例解析式为y=$\frac{8}{x}$;
(2)设平移后的直线交y轴于H.
∴S△ABH=S△ABC=18,
∵S△ABH=$\frac{1}{2}$×AH×4=18,
∴AH=9,
∵A(0,-2),
∴H(0,7),
∴平移后的直线的解析式为y=x+7.
点评 此题考查了一次函数与反比例函数的交点问题,涉及的知识有:一次函数与坐标轴的交点,待定系数法求函数解析式,三角形的面积求法,以及坐标与图形变化-平移,熟练掌握待定系数法是解本题的关键.

练习册系列答案
相关题目
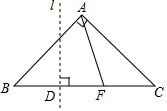 如图,等腰Rt△ABC中,AB=AC=1,点F是边BC上不与点B、C重合的一个动点,直线l垂直平分BF,垂足为D,当△AFC是等腰三角形时,BD的长为$\frac{\sqrt{2}}{4}$或$\frac{\sqrt{2}-1}{2}$.
如图,等腰Rt△ABC中,AB=AC=1,点F是边BC上不与点B、C重合的一个动点,直线l垂直平分BF,垂足为D,当△AFC是等腰三角形时,BD的长为$\frac{\sqrt{2}}{4}$或$\frac{\sqrt{2}-1}{2}$.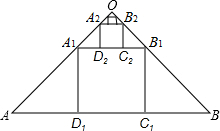 如图,等腰直角三角形OAB中,∠AOB=90°,AB=1,在△OAB中作内接正方形A1B1C1D1;在等腰直角三角形OA1B1中,作内接正方形A2B2C2D2;在等腰直角三角形OA2B2中,作内接正方形A3B3C3D3…;依次作下去,则第n个正方形AnBnCnDn的面积是$\frac{1}{{9}^{n}}$.
如图,等腰直角三角形OAB中,∠AOB=90°,AB=1,在△OAB中作内接正方形A1B1C1D1;在等腰直角三角形OA1B1中,作内接正方形A2B2C2D2;在等腰直角三角形OA2B2中,作内接正方形A3B3C3D3…;依次作下去,则第n个正方形AnBnCnDn的面积是$\frac{1}{{9}^{n}}$.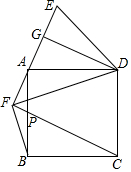 如图,正方形ABCD,过A作直线AE,作DG⊥AE,AG=GE,连接DE.
如图,正方形ABCD,过A作直线AE,作DG⊥AE,AG=GE,连接DE.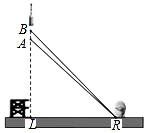 2016年11月3日,我国第一枚大型运载火箭“长征5号”在海南文昌航天发射场顺利升空,这标志着我国从航天大国迈向航天强国.如图,火箭从地面L处发射,当火箭到达A点时,从位于地面R处雷达站测得AR的距离是6km,仰角为42.4°;1秒后火箭到达B点,此时测得仰角为45.5°.
2016年11月3日,我国第一枚大型运载火箭“长征5号”在海南文昌航天发射场顺利升空,这标志着我国从航天大国迈向航天强国.如图,火箭从地面L处发射,当火箭到达A点时,从位于地面R处雷达站测得AR的距离是6km,仰角为42.4°;1秒后火箭到达B点,此时测得仰角为45.5°.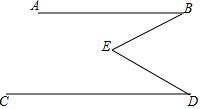 如图,已知∠BED=∠B+∠D,试说明AB∥CD.
如图,已知∠BED=∠B+∠D,试说明AB∥CD.