题目内容
11.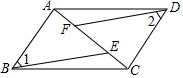 四边形ABCD是平行四边形,AF=CE,求证:∠1=∠2.
四边形ABCD是平行四边形,AF=CE,求证:∠1=∠2.
分析 由已知条件可得AE=FC,∠ABE=∠DCF,由SAS证明△BAE≌△DCF,从而得出结论.
解答 证明:∵AF=CE,
∴AF+EF=CE+EF,
即AE=CF,
∵四边形ABCD是平行四边形,
∴AB∥CD且AB=CD,
∴∠BAE=∠DCF,
在△BAE和△DCF中,$\left\{\begin{array}{l}{AB=CD}&{\;}\\{∠BAE=∠DCF}&{\;}\\{AE=CF}&{\;}\end{array}\right.$,
∴△BAE≌△DCF(SAS),
∴∠1=∠2.
点评 本题考查了平行四边形的性质、全等三角形的判定与性质;证得△BAE≌△DCF是解决问题的关键.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
20.某校对九年级全部240名学生的血型作了调查,列出统计表,则该校九年级O型血的学生有36人.
| 组别 | A型 | B型 | AB型 | O 型 |
| 频率 | 0.4 | 0.35 | 0.1 | 0.15 |

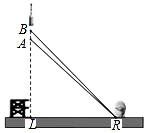 2016年11月3日,我国第一枚大型运载火箭“长征5号”在海南文昌航天发射场顺利升空,这标志着我国从航天大国迈向航天强国.如图,火箭从地面L处发射,当火箭到达A点时,从位于地面R处雷达站测得AR的距离是6km,仰角为42.4°;1秒后火箭到达B点,此时测得仰角为45.5°.
2016年11月3日,我国第一枚大型运载火箭“长征5号”在海南文昌航天发射场顺利升空,这标志着我国从航天大国迈向航天强国.如图,火箭从地面L处发射,当火箭到达A点时,从位于地面R处雷达站测得AR的距离是6km,仰角为42.4°;1秒后火箭到达B点,此时测得仰角为45.5°.