题目内容
若(4x2+2x)(x+a)的运算结果中不含x2的项,则a的值为_______.
-
【解析】【解析】
．∵运算结果中不含x2的项，∴4a+2=0，∴a=．故答案为： ．
练习册系列答案
阅读快车系列答案
相关题目
利用尺规作三角形,有三种基本类型:
(1)已知三角形的两边及其夹角,求作符合要求的三角形,其作图依据是“____”;
(2)已知三角形的两角及其夹边,求作符合要求的三角形,其作图依据是“____”;
(3)已知三角形的三边,求作符合要求的三角形,其作图依据是“____”.
SAS ASA SSS
【解析】根据SAS—两边及其夹角分别相等的两个三角形全等；ASA—两角及其夹边分别相等的两个三角形全等；SSS—三边分别相等的两个三角形全等.
故答案：(1)SAS、 (2)ASA 、(3)SSS. 已知tanβ=22.3，则β=_________（精确到1″）
87°25′56″
【解析】试题分析：利用计算器首先按2ndF，再按tan，再输入22.3，再按DMS即可得出答案．
∵tanβ=22.3，∴β=87°25′56″．
故答案为：87°25′56″ 下面四个数中，最大的是（ ）
A.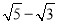 
B. sin88° C. tan46° D.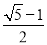 
C
【解析】试题分析：A、≈2.236-1.732≈0.504；
B、sin88°≈0.999；
C、tan46°≈1.036；
D、 ≈ ≈0.568．
故tan46°最大，
故选：C． 在一次实验中，小明把一根弹簧的上端固定、在其下端悬挂物体，下面是测得的弹簧的长度y与所挂物体质量x的一组对应值．
所挂物体质量x/kg | 0 | 1 | 2 | 3 | 4 | 5 |
弹簧长度y/cm | 18 | 20 | 22 | 24 | 26 | 28 |
①上表反映了哪两个变量之间的关系？哪个是自变量？哪个是因变量？
②当所挂物体重量为3千克时，弹簧多长？不挂重物时呢？
③若所挂重物为7千克时（在允许范围内），你能说出此时的弹簧长度吗？
①上表反映了弹簧长度与所挂物体质量之间的关系；其中所挂物体质量是自变量，弹簧长度是因变量；②当所挂物体重量为3千克时，弹簧长24厘米；当不挂重物时，弹簧长18厘米；③32厘米．
【解析】试题分析：①因为表中的数据主要涉及到弹簧的长度和所挂物体的质量，所以反映了所挂物体的质量和弹簧的长度之间的关系，所挂物体的质量是自变量；弹簧的长度是因变量；
②由表可知，当物体的质量为3kg时，弹簧的长... 有一游泳池注满水,现按一定速度将水排尽,然后进行清洗,再按相同速度注满清水,使用一段时间后,又按相同的速度将水排尽,则游泳池的存水量V(m3)随时间t(h)变化的大致图象是( )
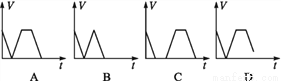
C
【解析】【解析】
根据题意分析可得：存水量V的变化有几个阶段：
1、减小为0，并持续一段时间；
2、增加至最大，并持续一段时间；
3、减小为0．
故选A． 如图,在△ABC中,AB=AC,AD=BD=BC,则∠A的度数是( )
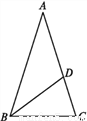
A. 30° B. 36° C. 45° D. 20°
B
【解析】【解析】
设∠A=x°．∵BD=AD，∴∠A=∠ABD=x°，∠BDC=∠A+∠ABD=2x°．
∵BD=BC，∴∠BDC=∠BCD=2x°．
∵AB=AC，∴∠ABC=∠BCD=2x°．
在△ABC中，x+2x+2x=180，解得：x=36，∴∠A=36°．
故选B． 若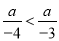
，试判断a的正负性．
a为负数
【解析】分析：先根据不等式基本性质3,两边都乘以,再根据不等式基本性质1,两边都减去3a即可得出结论.
本题解析：根据不等式基本性质3，两边都乘以－12，得3a＞4a．
根据不等式基本性质1，两边都减去3a，得0＞a ，即a<0 ，即a为负数． 已知等腰△ABC中，AB=AC，D是BC边上一点，连接AD，若△ACD和△ABD都是等腰三角形，则∠C的度数是 ．
36°或45°．
【解析】
试题分析：△ACD和△ABD都是等腰三角形，但没有说具体的边相等，所以应分情况讨论．
（1）AD=BD，DC=AD，那么△ADB和△ADC是全等三角形，可求得∠ADC=90°，那么∠C=45°；
（2）AB=BD，CD=AD，那么∠B=∠C=∠DAC，∠BAD=∠BDA=2∠C，然后用∠C表示出△ABC的内角和，即可求得5∠C=180°，那么∠C...