题目内容
解下列方程:
(1)4x-3(20-x)=6x-7(11-x);
(2)361(-x+1)2=16;
(3)2(x-1)3=-
;
(4)
-1=
-
.
(1)4x-3(20-x)=6x-7(11-x);
(2)361(-x+1)2=16;
(3)2(x-1)3=-
| 125 |
| 4 |
(4)
| 2x+1 |
| 4 |
| 2x-1 |
| 3 |
| 10x+1 |
| 12 |
考点:立方根,平方根,解一元一次方程
专题:
分析:(1)根据解一元一次方程的一般步骤,可得方程的解;
(2)根据等式的性质,可化成平方的形式,根据开平方,可得答案;
(3)根据等式的性质,可化成立方的形式,根据开立方,可得答案;
(4)根据解一元一次方程的一般步骤,可得方程的解.
(2)根据等式的性质,可化成平方的形式,根据开平方,可得答案;
(3)根据等式的性质,可化成立方的形式,根据开立方,可得答案;
(4)根据解一元一次方程的一般步骤,可得方程的解.
解答:解(1)去括号得4x-60+3x=6x-77+7x
移项得4x+3x-6x-7x=-77+60
合并同类项得-6x=-17,
系数化为1得x=
;
(2)方程两边都除以361,得(-x+1)2=
-x+1=±
x=
或x=
;
(3)方程两边都除以2得(x-1)3=-
,
x-1=-
x=-
;
(4)去分母得6x+3-12=8x-4-(10x+1)
移项得6x-8x+10x=-4-1-3+12
合并同类项得8x=4,
系数化为1得x=
.
移项得4x+3x-6x-7x=-77+60
合并同类项得-6x=-17,
系数化为1得x=
| 17 |
| 6 |
(2)方程两边都除以361,得(-x+1)2=
| 16 |
| 361 |
-x+1=±
| 4 |
| 19 |
x=
| 23 |
| 19 |
| 15 |
| 19 |
(3)方程两边都除以2得(x-1)3=-
| 125 |
| 8 |
x-1=-
| 5 |
| 2 |
x=-
| 3 |
| 2 |
(4)去分母得6x+3-12=8x-4-(10x+1)
移项得6x-8x+10x=-4-1-3+12
合并同类项得8x=4,
系数化为1得x=
| 1 |
| 2 |
点评:本题考查了了立方根,先化成立方的形式,再开立方,注意移项要变号.

练习册系列答案
相关题目
 如图,点E在正方形ABCD内,AE=6,BE=8,AB=10.试求出阴影部分的面积S.
如图,点E在正方形ABCD内,AE=6,BE=8,AB=10.试求出阴影部分的面积S. 如图,在△ABC中,∠B=60°,∠BAC与∠BCA的平分线AD、CE分别交BC和AB于点D、E,AD与CE相交于点F,求证:FE=FD.
如图,在△ABC中,∠B=60°,∠BAC与∠BCA的平分线AD、CE分别交BC和AB于点D、E,AD与CE相交于点F,求证:FE=FD.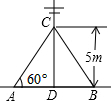 如图,在离地面高度5米的C处引拉线固定电线杆,拉线和地面成60°角,求拉线AC的长以及拉线下端点A与杆底D的距离AD (精确到0.01米).
如图,在离地面高度5米的C处引拉线固定电线杆,拉线和地面成60°角,求拉线AC的长以及拉线下端点A与杆底D的距离AD (精确到0.01米). 如图,在矩形ABCD中,点E、F分别在边AD、DC上,△ABE∽△DEF,AB=6,AE=9,DE=2,求EF的长.
如图,在矩形ABCD中,点E、F分别在边AD、DC上,△ABE∽△DEF,AB=6,AE=9,DE=2,求EF的长.
 在平行四边形ABCD中,点E、F分别在AB、CD上,且AE=CF.
在平行四边形ABCD中,点E、F分别在AB、CD上,且AE=CF.