题目内容
 如图,在△ABC中,∠B=60°,∠BAC与∠BCA的平分线AD、CE分别交BC和AB于点D、E,AD与CE相交于点F,求证:FE=FD.
如图,在△ABC中,∠B=60°,∠BAC与∠BCA的平分线AD、CE分别交BC和AB于点D、E,AD与CE相交于点F,求证:FE=FD.考点:角平分线的性质,全等三角形的判定与性质
专题:证明题
分析:根据三角形的内角和定理和角平分线的定义求出∠AFE=60°,∠AFC=120°,在AC上截取AG=AE,利用“边角边”证明△AEF和△AGF全等,根据全等三角形对应角相等可得∠AFG=∠AFE,全等三角形对应边相等可得FE=FG,然后求出∠CFG=∠CFD=60°,再利用“角边角”证明△CDF和△CGF全等,根据全等三角形对应边相等可得FD=FG,从而得证.
解答: 证明:∵∠B=60°,
证明:∵∠B=60°,
∴∠BAC+∠BCA=180°-60°=120°,
∵AD、CE分别平分∠BAC与∠BCA,
∴∠FAC+∠FCA=
(∠BAC+∠BCA)=
×120°=60°,
∴∠AFE=60°,∠AFC=120°,
如图,在AC上截取AG=AE,
则在△AEF和△AGF中,
,
∴△AEF≌△AGF(SAS),
∴∠AFG=∠AFE=60°,FE=FG,
∴∠CFG=∠CFD=60°,
在△CDF和△CGF中,
,
∴△CDF≌△CGF(ASA),
∴FD=FG,
∴FE=FD.
 证明:∵∠B=60°,
证明:∵∠B=60°,∴∠BAC+∠BCA=180°-60°=120°,
∵AD、CE分别平分∠BAC与∠BCA,
∴∠FAC+∠FCA=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠AFE=60°,∠AFC=120°,
如图,在AC上截取AG=AE,
则在△AEF和△AGF中,
|
∴△AEF≌△AGF(SAS),
∴∠AFG=∠AFE=60°,FE=FG,
∴∠CFG=∠CFD=60°,
在△CDF和△CGF中,
|
∴△CDF≌△CGF(ASA),
∴FD=FG,
∴FE=FD.
点评:本题考查了角平分线的定义,全等三角形的判定与性质,作出辅助线构造成两对全等三角形是解题的关键,也是本题的难点.

练习册系列答案
相关题目
 如图,△ABC的顶点A、B、C均在⊙O上,∠OAC=20°,则∠ABC的度数是( )
如图,△ABC的顶点A、B、C均在⊙O上,∠OAC=20°,则∠ABC的度数是( )| A、40° | B、60° |
| C、70° | D、80° |
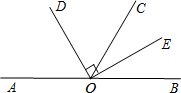 如图,点A、O、B在同一直线上,OD是∠AOC的平分线,OD⊥OE,且∠AOC=120°.
如图,点A、O、B在同一直线上,OD是∠AOC的平分线,OD⊥OE,且∠AOC=120°.
 如图,找一格点D,使得直线CD∥AB,找一格点F,使得直线CF⊥AB,画出直线CD,CF.
如图,找一格点D,使得直线CD∥AB,找一格点F,使得直线CF⊥AB,画出直线CD,CF.