题目内容
 如图,点E在正方形ABCD内,AE=6,BE=8,AB=10.试求出阴影部分的面积S.
如图,点E在正方形ABCD内,AE=6,BE=8,AB=10.试求出阴影部分的面积S.考点:勾股定理的逆定理
专题:
分析:由已知,根据勾股定理的逆定理得△ABE为直角三角形,用S阴影部分=S正方形ABCD-S△ABE求面积.
解答:解:在△ABE中,∵AE=6,BE=8,AB=10,
62+82=102,
∴△ABE是直角三角形,
∴S阴影部分=S正方形ABCD-S△ABE
=AB2-
×AE×BE
=100-
×6×8
=76.
故阴影部分的面积S是76.
62+82=102,
∴△ABE是直角三角形,
∴S阴影部分=S正方形ABCD-S△ABE
=AB2-
| 1 |
| 2 |
=100-
| 1 |
| 2 |
=76.
故阴影部分的面积S是76.
点评:本题考查了勾股定理的逆定理运用,正方形的性质.关键是判断△ABE为直角三角形,运用三角形面积公式求解.

练习册系列答案
相关题目
 如图,△ABC的顶点A、B、C均在⊙O上,∠OAC=20°,则∠ABC的度数是( )
如图,△ABC的顶点A、B、C均在⊙O上,∠OAC=20°,则∠ABC的度数是( )| A、40° | B、60° |
| C、70° | D、80° |
 如图,已知某市一座电视塔高AB为600米.张明在点C处测得电视塔塔顶B的仰角∠ACB=40°.
如图,已知某市一座电视塔高AB为600米.张明在点C处测得电视塔塔顶B的仰角∠ACB=40°.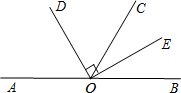 如图,点A、O、B在同一直线上,OD是∠AOC的平分线,OD⊥OE,且∠AOC=120°.
如图,点A、O、B在同一直线上,OD是∠AOC的平分线,OD⊥OE,且∠AOC=120°.