题目内容
18．
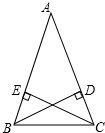如图，在△ABC中，AB=AC，CE，BD分别是AB，AC上的高．求证：BD=CE．
分析 利用面积法：根据S△ABC=$\frac{1}{2}$•AB•CE=$\frac{1}{2}$•AC•BD即可证明．也可以证明△EBC≌△CDB解决问题．
解答 证明：证法一：∵BD⊥AC，CE⊥AB，
∴S△ABC=$\frac{1}{2}$•AB•CE=$\frac{1}{2}$•AC•BD，
∵AB=AC
∴CE=BD．
证法二：∵AB=AC，
∴∠EBC=∠DCB，
在△BEC和△CDB中，
$\left\{\begin{array}{l}{∠BEC=∠CDB}\\{∠EBC=∠DCB}\\{BC=CB}\end{array}\right.$，
∴△EBC≌△CDB，
∴BD=CE．
点评 本题考查全等三角形的判定和性质、三角形的面积等知识，本题可以用面积法证明比较简单，也可以根据全等三角形的性质证明，属于基础题，是中考常考题型．
练习册系列答案
相关题目
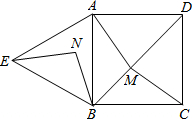如图，△ABE是等边三角形，M是正方形ABCD对角线BD（不含B点）上任意一点，BM=BN，∠ABN=15°（点N在AB的左侧），当AM+BM+CM的最小值为$\sqrt{3}$+1时，正方形的边长为$\sqrt{2}$．
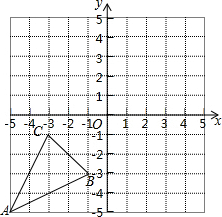如图，在平面直角坐标系中，△ABC的顶点坐标是A（-5，5），B（-1，-3），C（-3．-1）