题目内容
12.计算:(1)$\frac{{a}^{2}}{a-1}$-a-1;
(2)$\frac{1}{x-3}$-$\frac{6}{{x}^{2}-9}$-$\frac{x-1}{6-2x}$;
(3)$\frac{x+2}{{x}^{2}-2x}$-$\frac{x-1}{{x}^{2}-4x+4}$;
(4)$\frac{a-2}{{a}^{2}+2a}$+$\frac{a+1}{{a}^{2}+4a+4}$.
分析 (1)原式通分并利用同分母分式的减法法则计算即可得到结果;
(2)原式通分并利用同分母分式的减法法则计算即可得到结果;
(3)原式通分并利用同分母分式的减法法则计算即可得到结果;
(4)原式通分并利用同分母分式的加法法则计算即可得到结果.
解答 解:(1)原式=$\frac{{a}^{2}-(a+1)(a-1)}{a-1}$=$\frac{1}{a-1}$;
(2)原式=$\frac{2(x+3)}{2(x+3)(x-3)}$-$\frac{12}{2(x+3)(x-3)}$+$\frac{(x+3)(x-1)}{2(x+3)(x-3)}$=$\frac{2x+6-12+(x+3)(x-1)}{2(x+3)(x-3)}$=$\frac{{x}^{2}+4x-15}{2{x}^{2}-18}$;
(3)原式=$\frac{(x-2)(x+2)}{x(x-2)^{2}}$-$\frac{x(x-1)}{x(x-2)^{2}}$=$\frac{{x}^{2}-4-{x}^{2}+x}{x(x-2)^{2}}$=$\frac{x-4}{x(x-2)^{2}}$;
(4)原式=$\frac{{a}^{2}-4}{a(a+2)^{2}}$+$\frac{{a}^{2}+a}{a(a+2)^{2}}$=$\frac{2{a}^{2}+a-4}{a(a+2)^{2}}$.
点评 此题考查了分式的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.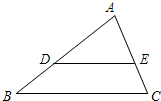 如图,△ABC中,DE∥BC,AD:DB=2:1,则△ADE与△ABC的面积之比是( )
如图,△ABC中,DE∥BC,AD:DB=2:1,则△ADE与△ABC的面积之比是( )
 如图,△ABC中,DE∥BC,AD:DB=2:1,则△ADE与△ABC的面积之比是( )
如图,△ABC中,DE∥BC,AD:DB=2:1,则△ADE与△ABC的面积之比是( )| A. | 4:1 | B. | 8:1 | C. | 4:9 | D. | 2:3 |
17.已知y=$\sqrt{x-2}$+$\sqrt{2-x}$-4,则$\sqrt{{y}^{x}}$的算术平方根的平方根是( )
| A. | ±2 | B. | 2 | C. | ±4 | D. | ±$\sqrt{2}$ |
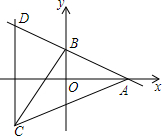 直线l:y=-$\frac{1}{2}$x+m与x,y轴的正半轴分别相交于点A、B,过点C(-4,-4)画平行于y轴的直线,交直线AB于点D,CD=10.
直线l:y=-$\frac{1}{2}$x+m与x,y轴的正半轴分别相交于点A、B,过点C(-4,-4)画平行于y轴的直线,交直线AB于点D,CD=10. 为了测量一池塘的宽AB,在岸边找到了一点C,使AC⊥AB,在AC上找到一点D,在BC上找到一点E,使DE⊥AC,测出AD=25m,DC=30m,DE=30m,那么你能算出池塘的宽AB吗?
为了测量一池塘的宽AB,在岸边找到了一点C,使AC⊥AB,在AC上找到一点D,在BC上找到一点E,使DE⊥AC,测出AD=25m,DC=30m,DE=30m,那么你能算出池塘的宽AB吗?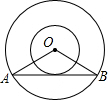 如图,⊙O的半径为8cm,圆内的弦AB=8$\sqrt{3}cm$,以点O为圆心,4cm为半径作小圆,求证:直线AB与小圆相切.
如图,⊙O的半径为8cm,圆内的弦AB=8$\sqrt{3}cm$,以点O为圆心,4cm为半径作小圆,求证:直线AB与小圆相切.