题目内容
17.已知y=$\sqrt{x-2}$+$\sqrt{2-x}$-4,则$\sqrt{{y}^{x}}$的算术平方根的平方根是( )| A. | ±2 | B. | 2 | C. | ±4 | D. | ±$\sqrt{2}$ |
分析 根据被开方数是非负数,可得x、y的值,根据开方运算,可得答案.
解答 解:由y=$\sqrt{x-2}$+$\sqrt{2-x}$-4,得
$\left\{\begin{array}{l}{x-2≥0}\\{2-x≥0}\\{\;}\end{array}\right.$,解得x=2.
当x=2时,y=-4,
$\sqrt{{y}^{x}}$=$\sqrt{(-4)^{2}}$=4,4的算术平方根是2,2的平方根是±$\sqrt{2}$,
故选:D.
点评 本题考查了二次根式有意义的条件,利用被开方数是非负数得出x、y的值是解题关键,注意先两次求算术平方根,再求平方根.

练习册系列答案
相关题目
7.若a<0,$\frac{a}{b}$<0,且|a|>|b|,则( )
| A. | a<-b<b<-a | B. | a<b<-b<-a | C. | -a<-b<b<a | D. | -b<-a<b<a |
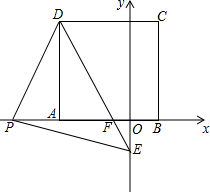 如图,在直角坐标系中,点A(-3,0)和点B(1,0)以AB为边在x轴上方作正方形ABCD,点P是x轴负半轴上一点,连接DP,过点P作DP的垂线与y轴负半轴交于点E,PD=PE,连接DE.
如图,在直角坐标系中,点A(-3,0)和点B(1,0)以AB为边在x轴上方作正方形ABCD,点P是x轴负半轴上一点,连接DP,过点P作DP的垂线与y轴负半轴交于点E,PD=PE,连接DE.