题目内容
2.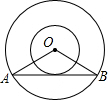 如图,⊙O的半径为8cm,圆内的弦AB=8$\sqrt{3}cm$,以点O为圆心,4cm为半径作小圆,求证:直线AB与小圆相切.
如图,⊙O的半径为8cm,圆内的弦AB=8$\sqrt{3}cm$,以点O为圆心,4cm为半径作小圆,求证:直线AB与小圆相切.
分析 过O作OC⊥AB于C,根据垂径定理得到AC=$\frac{1}{2}$AB=4$\sqrt{3}$cm,由勾股定理得到OC=$\sqrt{{8}^{2}-(4\sqrt{3})^{2}}$=4cm,即可得到结论.
解答  证明:过O作OC⊥AB于C,
证明:过O作OC⊥AB于C,
∴AC=$\frac{1}{2}$AB=4$\sqrt{3}$cm,
∵⊙O的半径为8cm,
∴OC=$\sqrt{{8}^{2}-(4\sqrt{3})^{2}}$=4cm,
∵4cm为半径作小圆,
∴直线AB与小圆相切.
点评 本题考查了切线的判定,垂径定理,勾股定理,正确的作出辅助线构造直角三角形是解题的关键.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
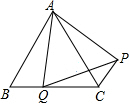 如图,点Q是等边△ABC的边BC上一点,以AQ为边作等边△AQP,求证:PC∥AB.
如图,点Q是等边△ABC的边BC上一点,以AQ为边作等边△AQP,求证:PC∥AB.