题目内容
9.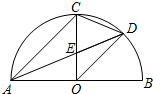 如图,AB是半圆直径,半径OC⊥AB于点O,AD平分∠CAB交弧BC于点D,AD与OC交于点E,连接CD、OD,给出以下四个结论:
如图,AB是半圆直径,半径OC⊥AB于点O,AD平分∠CAB交弧BC于点D,AD与OC交于点E,连接CD、OD,给出以下四个结论:①AC∥OD;②CE=OE;③∠CDE=∠COD;④2CD2=CE•AB.
其中正确结论的序号是①③④(在横线上填上你认为所有正确结论的代号).
分析 ①根据等腰三角形的性质和角平分线的性质,利用等量代换求证∠CAD=∠ADO即可;
②由①得OE:EC=OD:AC,再由OD≠AC,可得CE≠OE;
③根据圆周角定理得到∠CDE=$\frac{1}{2}$∠AOC=45°,根据角平分线的定义得到∠DAO=22.5°,求得∠COD=2∠CAD=45°,等量代换得到∠CDE=∠COD;
④根据同弧所对的圆周角等于它所对的圆心角的一半,求出∠COD=45°,再利用等腰三角形的性质和三角形内角和定理求出∠CDE=45°,再求证△CED∽△CDO,利用其对应变成比例即可得出结论.
解答 解:∵AB是半圆直径,
∴AO=OD,
∴∠OAD=∠ADO,
∵AD平分∠CAB交弧BC于点D,
∴∠CAD=∠DAO=$\frac{1}{2}$∠CAB,
∴∠CAD=∠ADO,
∴AC∥OD,故①正确.
由题意得,OD=R,AC=$\sqrt{2}$R,
∵OE:CE=OD:AC=$\frac{\sqrt{2}}{2}$,
∴OE≠CE,故②错误;
∵AB是半圆直径,半径OC⊥AB于点O,
∴∠AOC=∠COB=90°,
∴∠CDE=$\frac{1}{2}$∠AOC=45°,
∵OA=OC,
∴∠CAO=45°,
∵AD平分∠CAB交弧BC于点D,
∴∠DAO=22.5°,
∴∠COD=2∠CAD=45°,
∴∠CDE=∠COD;故③正确;
∵AD平分∠CAB交弧BC于点D,
∴∠CAD=$\frac{1}{2}$×45°=22.5°,
∴∠COD=45°,
∵AB是半圆直径,
∴OC=OD,
∴∠OCD=∠ODC=67.5°
∵∠CAD=∠ADO=22.5°(已证),
∴∠CDE=∠ODC-∠ADO=67.5°-22.5°=45°,
∴△CED∽△CDO,
∴$\frac{CD}{CO}=\frac{CE}{CD}$,
∴CD2=CO•CE=$\frac{1}{2}$AB•CE,
∴2CD2=CE•AB,故④正确.
综上可得①③④正确.
故答案为:①③④,
点评 本题考查了相似三角形的判定与性质,圆心角、弧、弦的关系,圆周角定理,等腰三角形的性质,三角形内角和定理等知识点的灵活运用,此题步骤繁琐,但相对而言,难易程度适中,很适合学生的训练是一道典型的题目.

 如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点,AD=6,AB=8,则$\frac{AF}{FC}$=( )
如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点,AD=6,AB=8,则$\frac{AF}{FC}$=( )| A. | $\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | $\frac{3}{2}$ | D. | $\frac{2}{3}$ |
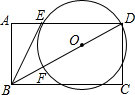 如图,在矩形ABCD中,点O在对角线BD上,以OD的长为半径的⊙O与AD、BD分别交于点E、F,且∠ABE=∠DBC.
如图,在矩形ABCD中,点O在对角线BD上,以OD的长为半径的⊙O与AD、BD分别交于点E、F,且∠ABE=∠DBC.
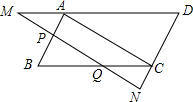 已知:?ABCD中,直线MN∥AC,分别交DA延长线于M,DC延长线于N,AB于P,BC于Q.求证:PM=QN.
已知:?ABCD中,直线MN∥AC,分别交DA延长线于M,DC延长线于N,AB于P,BC于Q.求证:PM=QN.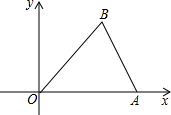 如图,已知A(3,0),B(2,3),将△OAB以点O为位似中心,相似比为2:1,放大得到△OA′B′,则顶点B的对应点B′的坐标为(-4,-6)或(4,6).
如图,已知A(3,0),B(2,3),将△OAB以点O为位似中心,相似比为2:1,放大得到△OA′B′,则顶点B的对应点B′的坐标为(-4,-6)或(4,6).