题目内容
19. 如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点,AD=6,AB=8,则$\frac{AF}{FC}$=( )
如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点,AD=6,AB=8,则$\frac{AF}{FC}$=( )| A. | $\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | $\frac{3}{2}$ | D. | $\frac{2}{3}$ |
分析 根据直角三角形的性质,可得CE与AE的关系,根据等腰三角形的性质,可得∠EAC=∠ECA,根据角平分线的定义,可得∠CAD=∠CAB,根据平行线的判定证出CE∥AD,得出△AFD∽△CFE,AD:CE=AF:CF;求得CE=4,即可解决问题.
解答 解:∵E是AB的中点,∠ACB=90°,
∴CE=$\frac{1}{2}$AB=AE,
∴∠EAC=∠ECA.
∵AC平分∠DAB,
∴∠CAD=∠CAB,
∴∠CAD=∠ECA,
∴CE∥AD;
∴△AFD∽△CFE,
∴AF:FC=AD:CE,
∵CE=$\frac{1}{2}$AB=4,AD=4,
∴$\frac{AF}{FC}$=$\frac{AD}{CE}$=$\frac{6}{4}$=$\frac{3}{2}$.
故选:C.
点评 本题考查了相似三角形的判定与性质,平行线的判定与性质、直角三角形斜边上的中线性质、等腰三角形的性质;证明三角形相似是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.下列等式中,是一元一次方程的是( )
| A. | x2-3x+2=0 | B. | 3+1=4 | C. | 2x=0 | D. | x+y=1 |
4.实数-5,0,$-\sqrt{3}$,3中最大的数是( )
| A. | 3 | B. | 0 | C. | $-\sqrt{3}$ | D. | -5 |
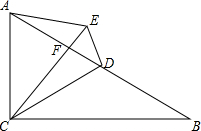 如图,在△ABC中,∠ACB=90°,∠B=30°,且点D是AB的中点,E为△ABC外一点,连接AE、DE,连接CE交AB于F,且∠CAD=∠CED.
如图,在△ABC中,∠ACB=90°,∠B=30°,且点D是AB的中点,E为△ABC外一点,连接AE、DE,连接CE交AB于F,且∠CAD=∠CED. 如图,已知直线AB∥DE.
如图,已知直线AB∥DE.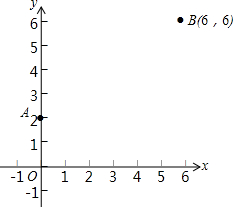 如图,已知A(0,2),B(6,6),x轴上一点C到A,B的距离之和为最小,求C点的坐标.
如图,已知A(0,2),B(6,6),x轴上一点C到A,B的距离之和为最小,求C点的坐标. 如图,正方形ABCD中,AB=1,点P是BC边上的任意一点(异于端点B、C),连接AP,过B、D两点作BE⊥AP于点E,DF⊥AP于点F.
如图,正方形ABCD中,AB=1,点P是BC边上的任意一点(异于端点B、C),连接AP,过B、D两点作BE⊥AP于点E,DF⊥AP于点F.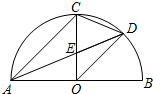 如图,AB是半圆直径,半径OC⊥AB于点O,AD平分∠CAB交弧BC于点D,AD与OC交于点E,连接CD、OD,给出以下四个结论:
如图,AB是半圆直径,半径OC⊥AB于点O,AD平分∠CAB交弧BC于点D,AD与OC交于点E,连接CD、OD,给出以下四个结论: