题目内容
17.方程2x2-3x-1=0的两根为x1,x2,则x12+x22=$\frac{13}{4}$.分析 根据根与系数的关系得出“x1+x2=-$\frac{b}{a}$=$\frac{3}{2}$,x1•x2=$\frac{c}{a}$=-$\frac{1}{2}$”,再利用完全平方公式将x12+x22转化成$({x}_{1}+{x}_{2})^{2}$-2x1•x2,代入数据即可得出结论.
解答 解:∵方程2x2-3x-1=0的两根为x1,x2,
∴x1+x2=-$\frac{b}{a}$=$\frac{3}{2}$,x1•x2=$\frac{c}{a}$=-$\frac{1}{2}$,
∴x12+x22=$({x}_{1}+{x}_{2})^{2}$-2x1•x2=$(\frac{3}{2})^{2}$-2×(-$\frac{1}{2}$)=$\frac{13}{4}$.
故答案为:$\frac{13}{4}$.
点评 本题考查了根与系数的关系以及完全平方公式,解题的关键是求出x1+x2=$\frac{3}{2}$,x1•x2=-$\frac{1}{2}$.本题属于基础题,难度不大,解决该题型题目时,根据根与系数的关系找出两根之和与两根之积,再利用完全平方公式将原代数式转化成只含两根之和与两根之积的代数式是关键.

练习册系列答案
相关题目
7.一元二次方程x2-3x-2=0的两根为x1,x2,则下列结论正确的是( )
| A. | x1=-1,x2=2 | B. | x1=1,x2=-2 | C. | x1+x2=3 | D. | x1x2=2 |
12.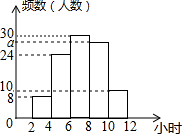 某校为了解全校同学五一假期参加社团活动的情况,抽查了100名同学,统计它们假期参加社团活动的时间,绘成频数分布直方图(如图),则参加社团活动时间的中位数所在的范围是( )
某校为了解全校同学五一假期参加社团活动的情况,抽查了100名同学,统计它们假期参加社团活动的时间,绘成频数分布直方图(如图),则参加社团活动时间的中位数所在的范围是( )
 某校为了解全校同学五一假期参加社团活动的情况,抽查了100名同学,统计它们假期参加社团活动的时间,绘成频数分布直方图(如图),则参加社团活动时间的中位数所在的范围是( )
某校为了解全校同学五一假期参加社团活动的情况,抽查了100名同学,统计它们假期参加社团活动的时间,绘成频数分布直方图(如图),则参加社团活动时间的中位数所在的范围是( )| A. | 4-6小时 | B. | 6-8小时 | C. | 8-10小时 | D. | 不能确定 |
2.某中学组织学生到商场参加社会实践活动,他们参与了某种品牌运动鞋的销售工作,已知该运动鞋每双的进价为120元,为寻求合适的销售价格进行了4天的试销,试销情况如表所示:
(1)观察表中数据,x,y满足什么函数关系?请求出这个函数关系式;
(2)若商场计划每天的销售利润为3000元,则其单价应定为多少元?
| 第1天 | 第2天 | 第3天 | 第4天 | |
| 售价x(元/双) | 150 | 200 | 250 | 300 |
| 销售量y(双) | 40 | 30 | 24 | 20 |
(2)若商场计划每天的销售利润为3000元,则其单价应定为多少元?
6.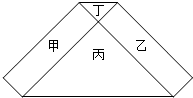 如图的六边形是由甲、乙两个长方形和丙、丁两个等腰直角三角形所组成,其中甲、乙的面积和等于丙、丁的面积和.若丙的一股长为2,且丁的面积比丙的面积小,则丁的一股长为何?( )
如图的六边形是由甲、乙两个长方形和丙、丁两个等腰直角三角形所组成,其中甲、乙的面积和等于丙、丁的面积和.若丙的一股长为2,且丁的面积比丙的面积小,则丁的一股长为何?( )
 如图的六边形是由甲、乙两个长方形和丙、丁两个等腰直角三角形所组成,其中甲、乙的面积和等于丙、丁的面积和.若丙的一股长为2,且丁的面积比丙的面积小,则丁的一股长为何?( )
如图的六边形是由甲、乙两个长方形和丙、丁两个等腰直角三角形所组成,其中甲、乙的面积和等于丙、丁的面积和.若丙的一股长为2,且丁的面积比丙的面积小,则丁的一股长为何?( )| A. | $\frac{1}{2}$ | B. | $\frac{3}{5}$ | C. | 2-$\sqrt{3}$ | D. | 4-2$\sqrt{3}$ |
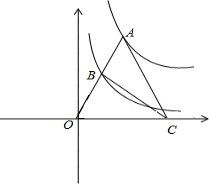 如图,点A为函数y=$\frac{9}{x}$(x>0)图象上一点,连结OA,交函数y=$\frac{1}{x}$(x>0)的图象于点B,点C是x轴上一点,且AO=AC,则△ABC的面积为6.
如图,点A为函数y=$\frac{9}{x}$(x>0)图象上一点,连结OA,交函数y=$\frac{1}{x}$(x>0)的图象于点B,点C是x轴上一点,且AO=AC,则△ABC的面积为6.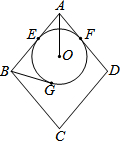 如图,菱形ABCD的边长为10,圆O分别与AB、AD相切于E、F两点,且与BG相切于G点.若AO=5,且圆O的半径为3,则BG的长度为何?( )
如图,菱形ABCD的边长为10,圆O分别与AB、AD相切于E、F两点,且与BG相切于G点.若AO=5,且圆O的半径为3,则BG的长度为何?( )