题目内容
9.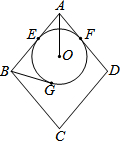 如图,菱形ABCD的边长为10,圆O分别与AB、AD相切于E、F两点,且与BG相切于G点.若AO=5,且圆O的半径为3,则BG的长度为何?( )
如图,菱形ABCD的边长为10,圆O分别与AB、AD相切于E、F两点,且与BG相切于G点.若AO=5,且圆O的半径为3,则BG的长度为何?( )| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
分析 连接OE,由⊙O与AB相切于E,得到∠AEO=90°,根据勾股定理得到AE=$\sqrt{A{O}^{2}-O{E}^{2}}$=4,根据切线长定理即可得到结论.
解答 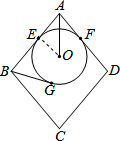 解:连接OE,
解:连接OE,
∵⊙O与AB相切于E,
∴∠AEO=90°,
∵AO=5,OE=3,
∴AE=$\sqrt{A{O}^{2}-O{E}^{2}}$=4,
∵AB=10,
∴BE=6,
∵BG与⊙O相切于G,
∴BG=BE=6,
故选C.
点评 本题考查了切线的性质,勾股定理,熟练掌握切线的性质是解题的关键.

练习册系列答案
相关题目
20. 如图,已知⊙O是等腰Rt△ABC的外接圆,点D是$\widehat{AC}$上一点,BD交AC于点E,若BC=4,AD=$\frac{4}{5}$,则AE的长是( )
如图,已知⊙O是等腰Rt△ABC的外接圆,点D是$\widehat{AC}$上一点,BD交AC于点E,若BC=4,AD=$\frac{4}{5}$,则AE的长是( )
 如图,已知⊙O是等腰Rt△ABC的外接圆,点D是$\widehat{AC}$上一点,BD交AC于点E,若BC=4,AD=$\frac{4}{5}$,则AE的长是( )
如图,已知⊙O是等腰Rt△ABC的外接圆,点D是$\widehat{AC}$上一点,BD交AC于点E,若BC=4,AD=$\frac{4}{5}$,则AE的长是( )| A. | 3 | B. | 2 | C. | 1 | D. | 1.2 |
4.若满足不等式20<5-2(2+2x)<50的最大整数解为a,最小整数解为b,则a+b之值为何?( )
| A. | -15 | B. | -16 | C. | -17 | D. | -18 |
14.算式[-5-(-11)]÷($\frac{3}{2}$×4)之值为何?( )
| A. | 1 | B. | 16 | C. | -$\frac{8}{3}$ | D. | -$\frac{128}{3}$ |


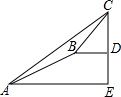 某数学兴趣小组同学进行测量大树CD高度的综合实践活动,如图,在点A处测得直立于地面的大树顶端C的仰角为36°,然后沿在同一剖面的斜坡AB行走13米至坡顶B处,然后再沿水平方向行走6米至大树脚底点D处,斜面AB的坡度(或坡比)i=1:2.4,那么大树CD的高度约为(参考数据:sin36°≈0.59,cos36°≈0.81,tan36°≈0.73)( )
某数学兴趣小组同学进行测量大树CD高度的综合实践活动,如图,在点A处测得直立于地面的大树顶端C的仰角为36°,然后沿在同一剖面的斜坡AB行走13米至坡顶B处,然后再沿水平方向行走6米至大树脚底点D处,斜面AB的坡度(或坡比)i=1:2.4,那么大树CD的高度约为(参考数据:sin36°≈0.59,cos36°≈0.81,tan36°≈0.73)( )