题目内容
当k=____________时,方程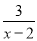 =2-
=2-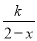 会产生增根.
会产生增根.
 3
【解析】=2-,去分母得: ,当x=2时,k=3.
故答案:3.
3
【解析】=2-,去分母得: ,当x=2时,k=3.
故答案:3.
练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
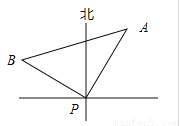
某时刻海上点P处有一客轮,测得灯塔A位于P的北偏东30°方向,且相距50海里.客轮以60海里/小时的速度沿北偏西60°方向航行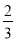 小时到达B处,那么tan∠BAP=( )
小时到达B处,那么tan∠BAP=( )
A. 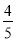 B.
B. 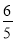 C.
C. 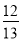 D.
D. 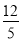
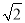
 A
【解析】试题分析:∵灯塔A位于客轮P的北偏东30°方向,且相距50海里,∴PA=50,
∵客轮以60海里/小时的速度沿北偏西60°方向航行小时到达B处,
∴∠APB=90° BP=60×=40, ∴tan∠BAP=,故选A.
A
【解析】试题分析:∵灯塔A位于客轮P的北偏东30°方向,且相距50海里,∴PA=50,
∵客轮以60海里/小时的速度沿北偏西60°方向航行小时到达B处,
∴∠APB=90° BP=60×=40, ∴tan∠BAP=,故选A. 一个多边形的每个外角都是36°,这个多边形是______边形
 十
【解析】∵任何多边形的外角和等于360°,
∴多边形的边数为360°÷36°=10,
故答案为:十.
十
【解析】∵任何多边形的外角和等于360°,
∴多边形的边数为360°÷36°=10,
故答案为:十. 解方程:
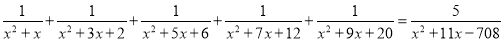 .
.
 x=118
【解析】【试题分析】用拆项法解方程, = 将方程左边化简为= ,再解分式方程即可.
【试题解析】
因为方程的左边
=
=
=
=
故原方程可变为.
所以.
解得.
经检验是原方程的根.
x=118
【解析】【试题分析】用拆项法解方程, = 将方程左边化简为= ,再解分式方程即可.
【试题解析】
因为方程的左边
=
=
=
=
故原方程可变为.
所以.
解得.
经检验是原方程的根. 若关于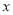 的方程
的方程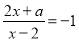 的解为正数,则
的解为正数,则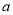 的取值范围是_____.
的取值范围是_____.
 且
【解析】解方程得: ,因为它的解是正数,则 ,得且.
故答案: 且.
且
【解析】解方程得: ,因为它的解是正数,则 ,得且.
故答案: 且. 如果方程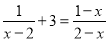 有增根, 那么增根是_______.
有增根, 那么增根是_______.
 x=2
【解析】∵原方程有增根,
∴最简公分母x-2=0,
解得x=2,
故答案为:x=2.
x=2
【解析】∵原方程有增根,
∴最简公分母x-2=0,
解得x=2,
故答案为:x=2. 下列关于x的方程是分式方程的是( )
A. 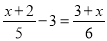 ; B.
; B. 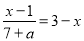 ; C.
; C. 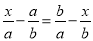 ; D.
; D. 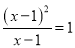
 D
【解析】根据分式方程的定义——分母中含有未知数的方程.故选D.
D
【解析】根据分式方程的定义——分母中含有未知数的方程.故选D. 计算.
(1)  ;
;
(2)  ;
;
(3)(4x2-y2)÷ .
.
 (1)- ;(2)8x2+10x-3;(3)2x+y.
【解析】试题分析:按照分式混合运算的顺序进行运算即可.
试题解析:
(1)
(2)原式
(3)
(1)- ;(2)8x2+10x-3;(3)2x+y.
【解析】试题分析:按照分式混合运算的顺序进行运算即可.
试题解析:
(1)
(2)原式
(3) 如图,在四边形ABCD中,P是BC边上一点,∠A=∠B=90º,E为AB的中点,连接DP,EP.若FG为△DPE的中位线,AB=AD=4,则FG=___________.
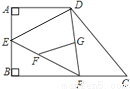
 【解析】∵点E是AB的中点,AB=4,
∴AE=AB=2.
∵∠A=90°,
∴DE=.
∵FG是△EDP的中位线,
∴FG=ED=.
【解析】∵点E是AB的中点,AB=4,
∴AE=AB=2.
∵∠A=90°,
∴DE=.
∵FG是△EDP的中位线,
∴FG=ED=.