题目内容
某学校用420元钱到商场去购买“84”消毒液,经过还价,每瓶便宜0.5元,结果比用原价多买了20瓶,求原价每瓶多少元?若设原价每瓶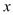 元,则可列出方程为( )
元,则可列出方程为( )
A. 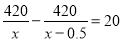 B.
B. 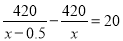
C. 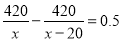 D.
D. 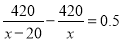
 B
【解析】设原价每瓶x元,根据某校用420元钱到商场去购买“84”消毒液,经过还价,每瓶便宜0.5元,结果比用原价多买了20瓶,可列方程.
【解析】
设原价每瓶x元,
=20.
故选B.
B
【解析】设原价每瓶x元,根据某校用420元钱到商场去购买“84”消毒液,经过还价,每瓶便宜0.5元,结果比用原价多买了20瓶,可列方程.
【解析】
设原价每瓶x元,
=20.
故选B.
练习册系列答案
相关题目
解方程:
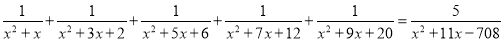 .
.
 x=118
【解析】【试题分析】用拆项法解方程, = 将方程左边化简为= ,再解分式方程即可.
【试题解析】
因为方程的左边
=
=
=
=
故原方程可变为.
所以.
解得.
经检验是原方程的根.
x=118
【解析】【试题分析】用拆项法解方程, = 将方程左边化简为= ,再解分式方程即可.
【试题解析】
因为方程的左边
=
=
=
=
故原方程可变为.
所以.
解得.
经检验是原方程的根. 计算.
(1)  ;
;
(2)  ;
;
(3)(4x2-y2)÷ .
.
 (1)- ;(2)8x2+10x-3;(3)2x+y.
【解析】试题分析:按照分式混合运算的顺序进行运算即可.
试题解析:
(1)
(2)原式
(3)
(1)- ;(2)8x2+10x-3;(3)2x+y.
【解析】试题分析:按照分式混合运算的顺序进行运算即可.
试题解析:
(1)
(2)原式
(3) 解下列方程:
(1)1﹣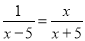 (2)
(2)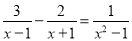 .
.
 (1) ;(2)x=-5
【解析】试题分析:先去分母,把分式方程转化为整式方程,然后按照整式方程的解法求解,求出未知数的值后要验根.
【解析】
(1)去分母得:x2﹣25﹣x﹣5=x2﹣5x,
解得:x=,
经检验x=是分式方程的解;
(2)去分母得:3x+3﹣2x+3=1,
解得:x=﹣5,
经检验x=﹣5是分式方程的解.
(1) ;(2)x=-5
【解析】试题分析:先去分母,把分式方程转化为整式方程,然后按照整式方程的解法求解,求出未知数的值后要验根.
【解析】
(1)去分母得:x2﹣25﹣x﹣5=x2﹣5x,
解得:x=,
经检验x=是分式方程的解;
(2)去分母得:3x+3﹣2x+3=1,
解得:x=﹣5,
经检验x=﹣5是分式方程的解. 填空:  =1÷(____),
=1÷(____),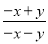 =﹣(____) ÷(x+y).
=﹣(____) ÷(x+y).
 x-y, -x+y
【解析】=1÷=1÷(x-y), ==﹣(-x+y) ÷(x+y).
x-y, -x+y
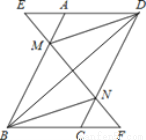
【解析】=1÷=1÷(x-y), ==﹣(-x+y) ÷(x+y). 如图所示,在平行四边形ABCD中,延长DA到点E,延长BC到点F,使得AE=CF,连接EF,分别交AB,CD于点M,N,连接DM,BN.
(1)求证:△AEM≌△CFN;
(2)求证:BD与MN互相平分.
 (1)证明见解析(2)证明见解析
【解析】试题分析:(1)先根据平行四边形的性质可得出AD∥BC,∠DAB=∠BCD,再根据平行线的性质及补角的性质得出∠E=∠F,∠EAM=∠FCN,从而利用ASA可作出证明;
(2)根据平行四边形的性质及(1)的结论可得BM 平行且等于DN,则由有一组对边平行且相等的四边形是平行四边形可得四边形BMDN是平行四边形,再由平行四边形的性质即可证明结论....
(1)证明见解析(2)证明见解析
【解析】试题分析:(1)先根据平行四边形的性质可得出AD∥BC,∠DAB=∠BCD,再根据平行线的性质及补角的性质得出∠E=∠F,∠EAM=∠FCN,从而利用ASA可作出证明;
(2)根据平行四边形的性质及(1)的结论可得BM 平行且等于DN,则由有一组对边平行且相等的四边形是平行四边形可得四边形BMDN是平行四边形,再由平行四边形的性质即可证明结论.... 如图,在四边形ABCD中,P是BC边上一点,∠A=∠B=90º,E为AB的中点,连接DP,EP.若FG为△DPE的中位线,AB=AD=4,则FG=___________.
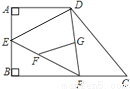
 【解析】∵点E是AB的中点,AB=4,
∴AE=AB=2.
∵∠A=90°,
∴DE=.
∵FG是△EDP的中位线,
∴FG=ED=.
【解析】∵点E是AB的中点,AB=4,
∴AE=AB=2.
∵∠A=90°,
∴DE=.
∵FG是△EDP的中位线,
∴FG=ED=. “五一”江北水城文化旅游节期间,几名同学包租一辆面包车前去旅游,面包车的租价为180元,出发时又增加了两名同学,结果每个同学比原来少摊了3元钱车费,设参加游览的同学共x人,应该如何列出方程?(不用求解,只列出即可)
 【解析】分析:设原来参加游览的同学共x人,面包车的租价为180元,出发时又增加了两名同学,结果每个同学比原来少摊了3元钱车费,可列方程.
本题解析:设参加游览的同学共x人,那么出发前为x—2人,
根据题意可以得出
【解析】分析:设原来参加游览的同学共x人,面包车的租价为180元,出发时又增加了两名同学,结果每个同学比原来少摊了3元钱车费,可列方程.
本题解析:设参加游览的同学共x人,那么出发前为x—2人,
根据题意可以得出 化简:  +
+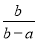 -
-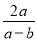 =___.
=___.
 -1
【解析】试题解析:原式
故答案为:
-1
【解析】试题解析:原式
故答案为: 
