题目内容
计算: 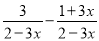
 1
【解析】试题分析:根据分式加减的运算法则进行运算即可.
试题解析:原式
1
【解析】试题分析:根据分式加减的运算法则进行运算即可.
试题解析:原式
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
关于x的分式方程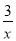 +
+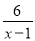 -
-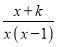 =0有解,则k满足( )
=0有解,则k满足( )
A. k≠-3 B. k≠5
C. k≠-3且k≠-5 D. k≠-3且k≠5
 D
【解析】原分式方程去分母,得
3(x-1)+6x=x+k,
整理,得
8x-k-3=0,
解得
x=,
要使分式方程不会产生增根,则x≠0且x≠1,
∴≠0且≠1.
解得,k≠-3且k≠5
故选D.
D
【解析】原分式方程去分母,得
3(x-1)+6x=x+k,
整理,得
8x-k-3=0,
解得
x=,
要使分式方程不会产生增根,则x≠0且x≠1,
∴≠0且≠1.
解得,k≠-3且k≠5
故选D. 已知关于x的分式方程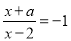 的根大于零,那么a的取值范围是_____________
的根大于零,那么a的取值范围是_____________
 a<2且a≠-2
【解析】方程两边都乘(x-2)得,x+a=2-x,
解得x=.∵根大于0, ∴>0, ∴a<2, ∵x-2≠0, ∴-2≠0,
解得:a≠-2, ∴a的取值范围是a<2且a≠-2.故答案为: a<2且a≠-2.
a<2且a≠-2
【解析】方程两边都乘(x-2)得,x+a=2-x,
解得x=.∵根大于0, ∴>0, ∴a<2, ∵x-2≠0, ∴-2≠0,
解得:a≠-2, ∴a的取值范围是a<2且a≠-2.故答案为: a<2且a≠-2. 计算: 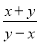 +
+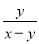 -
-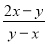
 1
【解析】试题分析:根据分式加减的运算法则进行运算即可.
试题解析:原式
1
【解析】试题分析:根据分式加减的运算法则进行运算即可.
试题解析:原式 若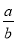 =
=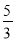 ,则
,则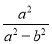 +
+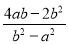 +
+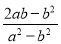 的值为( )
的值为( )
A. 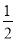 B.
B. 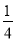 C. 2 D. 4
C. 2 D. 4
 B
【解析】++
=-+
=
=
=.
∵=,
∴设a=5k,b=3k,
∴原式==.
故选B.
B
【解析】++
=-+
=
=
=.
∵=,
∴设a=5k,b=3k,
∴原式==.
故选B. 计算: 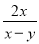 +
+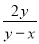 =__
=__
 2
【解析】试题解析:原式
故答案为:2.
2
【解析】试题解析:原式
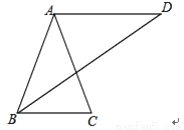
故答案为:2. 如图,已知AB=AC=AD,且AD∥BC,求证:∠C=2∠D.
 证明见解析.
【解析】试题分析:首先根据AB=AC=AD,可得∠C=∠ABC,∠D=∠ABD,∠ABC=∠CBD+∠D;然后根据AD∥BC,可得∠CBD=∠D,据此判断出∠ABC=2∠D,再根据∠C=∠ABC,即可判断出∠C=2∠D.
试题解析:∵AB=AC=AD,
∴∠C=∠ABC,∠D=∠ABD.
∴∠ABC=∠CBD+∠D.
∵AD∥BC,
∴∠CBD=∠...
证明见解析.
【解析】试题分析:首先根据AB=AC=AD,可得∠C=∠ABC,∠D=∠ABD,∠ABC=∠CBD+∠D;然后根据AD∥BC,可得∠CBD=∠D,据此判断出∠ABC=2∠D,再根据∠C=∠ABC,即可判断出∠C=2∠D.
试题解析:∵AB=AC=AD,
∴∠C=∠ABC,∠D=∠ABD.
∴∠ABC=∠CBD+∠D.
∵AD∥BC,
∴∠CBD=∠... 如图,在△ABC中,∠B=∠C,AB=5,则AC的长为( )

A.2 B.3 C.4 D.5
 D
【解析】
根据等腰三角形的性质可得AB=AC,继而得出AC的长.
【解析】
∵∠B=∠C,
∴AB=AC=5.
故选D.
D
【解析】
根据等腰三角形的性质可得AB=AC,继而得出AC的长.
【解析】
∵∠B=∠C,
∴AB=AC=5.
故选D. (3a-b)(3a+b)-(2a-b)2
 5a2+4ab-2b2
【解析】试题分析:先根据平方差公式与完全平方公式分别计算,再合并同类项即可.
试题解析:
(3a-b)(3a+b)-(2a-b)2=9a2-b2-4a2+4ab-b2=5a2+4ab-2b2.
5a2+4ab-2b2
【解析】试题分析:先根据平方差公式与完全平方公式分别计算,再合并同类项即可.
试题解析:
(3a-b)(3a+b)-(2a-b)2=9a2-b2-4a2+4ab-b2=5a2+4ab-2b2.