题目内容
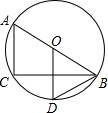 如图,AB是⊙O的直径,BC是弦,OD⊥BC于点E,交于点D.
如图,AB是⊙O的直径,BC是弦,OD⊥BC于点E,交于点D.(1)若BC=8,ED=2,求⊙O的半径;
(2)连接CD,设∠BDC=α,∠ABC=β,探究α与β之间的关系式,并给予适当的说明.
考点:垂径定理,勾股定理,圆周角定理
专题:
分析:(1)设⊙O的半径为r,则EO=r-2,在Rt△BOE中,根据勾股定理可得r2=42+(r-2)2,再解出r即可;
(2)连接CD,根据直径所对的圆周角为90°可得∠A+β=90°,根据圆内接四边形对角互补可得∠A+α=180°,进而可得α-β=90°.
(2)连接CD,根据直径所对的圆周角为90°可得∠A+β=90°,根据圆内接四边形对角互补可得∠A+α=180°,进而可得α-β=90°.
解答:解:(1)设⊙O的半径为r,即BO=DO=r,
∵ED=2,
∴EO=r-2,
∵DO⊥BC,
∴BE=CE=
BC=4,
在Rt△BOE中,r2=42+(r-2)2,
解得:r=5,
即⊙O的半径为5;
(2)α-β=90°,
理由:连接CD,
∵AB是⊙O的直径,
∴∠A+β=90°,
∵∠A+α=180°,
∴α-β=90°.
∵ED=2,
∴EO=r-2,
∵DO⊥BC,

∴BE=CE=
| 1 |
| 2 |
在Rt△BOE中,r2=42+(r-2)2,
解得:r=5,
即⊙O的半径为5;
(2)α-β=90°,
理由:连接CD,
∵AB是⊙O的直径,
∴∠A+β=90°,
∵∠A+α=180°,
∴α-β=90°.
点评:此题主要考查了垂径定理,圆周角定理,以及圆内接四边形,关键是掌握垂径定理:平分弦的直径平分这条弦,并且平分弦所对的两条弧.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列说法正确的是( )
①点(0,0)是坐标原点;②点(2,3)和点(3,2)是同一个点;③点(0,-3)在y轴上.
①点(0,0)是坐标原点;②点(2,3)和点(3,2)是同一个点;③点(0,-3)在y轴上.
| A、1个 | B、2个 | C、3个 | D、0个 |
 如图所示,△ABC为等边三角形,D、E分别是AC、BC上的点,且AD=CE,AE与BD相交于点P,BF⊥AE于F,求证:BP=2PF.
如图所示,△ABC为等边三角形,D、E分别是AC、BC上的点,且AD=CE,AE与BD相交于点P,BF⊥AE于F,求证:BP=2PF. 如图,点O是正六边形ABCDEF的中心,点O到正六边形的一边的距离为6,求这个正六边形的周长和面积.
如图,点O是正六边形ABCDEF的中心,点O到正六边形的一边的距离为6,求这个正六边形的周长和面积. 如图,AB是⊙O的直径,且AD∥OC,若弧AD的度数为80°,求弧CD的度数.
如图,AB是⊙O的直径,且AD∥OC,若弧AD的度数为80°,求弧CD的度数.