题目内容
如果二次函数y=ax2+bx+c的图象的顶点坐标是(2,4),且直线y=x+4依次与y轴和抛物线相交于P、Q、R三点,PQ:QR=1:3,则这个二次函数解析式为 .
考点:二次函数综合题
专题:
分析:根据二次函数y=ax2+bx+c的图象的顶点坐标是(2,4),利用顶点法设该二次函数解析式为y=a(x-2)2+4.根据直线y=x+4依次与y轴和抛物线相交于P、Q、R三点,则可确定P点的坐标,并设Q、R点的坐标为(x1,y1)和(x2,y2).根据两点间的距离公式与PQ:QR=1:3求得|x2|与|x1|的比值.直线y=x+4与抛物线相交于Q、R两点列出方程a(x-2)2+4=x+4,利用一元二次方程根与系数的关系,可求出x1、x2、a的值.因此抛物线即可确定.
解答:解:∵图象的顶点坐标是(2,4),
∴所以二次函数解析式为y=a(x-2)2+4 ①,
∵直线y=x+4依次与y轴和抛物线相交于P、Q、R三点,
∴P点的坐标是(0,4),设Q、R点的坐标为(x1,y1)和(x2,y2),则y1=x1+4,y2=x2+4,
∵|PQ|=
=
=
|x1|,
|PR|=
=
=
|x2|,
∵PQ:QR=1:3且P在QR之处,
∴PQ:PR=PQ:(PQ+QR)=1:4,
|x1|:
|x2|=1:4,
∴|x2|=4|x1|②,
又x1,x2是抛物线与直线交点的横坐标,
∴a(x-2)2+4=x+4,即ax2-(4a+1)x+4a=0,
∴a(x2-
x+4)=0,
由韦达定理,
,
由③得,x1、x2同号,再由②得 x2=4x1,
∴x1=±1,x2=±4,从④得a=1,或a=-
∴y=x2-4x+8或y=-
x2+
x+
,
故答案为:y=x2-4x+8或y=-
x2+
x+
.
∴所以二次函数解析式为y=a(x-2)2+4 ①,
∵直线y=x+4依次与y轴和抛物线相交于P、Q、R三点,
∴P点的坐标是(0,4),设Q、R点的坐标为(x1,y1)和(x2,y2),则y1=x1+4,y2=x2+4,
∵|PQ|=
| (x1-0)2+(y1-4)2 |
| x12+x12 |
| 2 |
|PR|=
| (x22-0)2+(y2-4)2 |
| x22+x22 |
| 2 |
∵PQ:QR=1:3且P在QR之处,
∴PQ:PR=PQ:(PQ+QR)=1:4,
| 2 |
| 2 |
∴|x2|=4|x1|②,
又x1,x2是抛物线与直线交点的横坐标,
∴a(x-2)2+4=x+4,即ax2-(4a+1)x+4a=0,
∴a(x2-
| 4a+1 |
| a |
由韦达定理,
|
由③得,x1、x2同号,再由②得 x2=4x1,
∴x1=±1,x2=±4,从④得a=1,或a=-
| 1 |
| 9 |
∴y=x2-4x+8或y=-
| 1 |
| 9 |
| 4 |
| 9 |
| 32 |
| 9 |
故答案为:y=x2-4x+8或y=-
| 1 |
| 9 |
| 4 |
| 9 |
| 32 |
| 9 |
点评:本题主要考查了二次函数与方程、几何知识的综合应用,其中涉及到的知识点有抛物线的顶点公式和相似三角形的性质、一元二次方程根与系数的关系.解题的关键是利用数形结合的数学思想方法.

练习册系列答案
相关题目
在实数0、3、-
、2.236、π、3.14中无理数的个数是( )
| 6 |
| A、1 | B、2 | C、3 | D、4 |
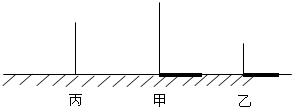 如图所示,甲物体高4米,影长3米,乙物体高2米,影长4米,两物体相距5米.
如图所示,甲物体高4米,影长3米,乙物体高2米,影长4米,两物体相距5米.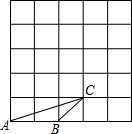 如图,在5×5的正方形方格中,△ABC的顶点都在边长为1的小正方形的顶点上,作一个与△ABC相似的△DEF,使它的三个顶点都在小正方形的顶点上,则△DEF的最大面积是
如图,在5×5的正方形方格中,△ABC的顶点都在边长为1的小正方形的顶点上,作一个与△ABC相似的△DEF,使它的三个顶点都在小正方形的顶点上,则△DEF的最大面积是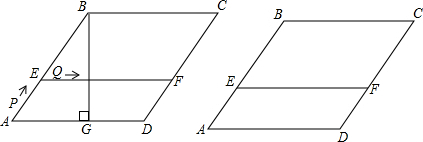
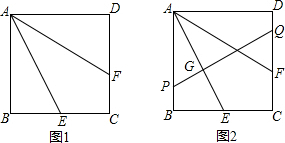
 如图所示,△ABC为等边三角形,D、E分别是AC、BC上的点,且AD=CE,AE与BD相交于点P,BF⊥AE于F,求证:BP=2PF.
如图所示,△ABC为等边三角形,D、E分别是AC、BC上的点,且AD=CE,AE与BD相交于点P,BF⊥AE于F,求证:BP=2PF.