题目内容
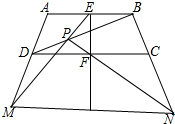如图，已知四边形ABCD，E是AB中点，F是CD中点，P是BD对角线上一点，EP延长线交AD延长线于点M，PF延长线交BC延长线于点N，证明：直线EF平分MN．考点：平行线分线段成比例
专题：证明题
分析：取BD中点G，连结EG、FG，延长ME到H，使HE=ME，连结HB、HN．由三角形中位线定理得出EG∥AD，GF∥BC．利用SAS证明△BEH≌△AEM（SAS），得到∠BHE=∠AME，于是BH∥AM，由EG∥AM，得出EG∥BH，根据平行线分线段成比例定理得出
=
，由GF∥BN，根据平行线分线段成比例定理得出
=
，那么
=
，EF∥HN．再设直线EF与MN交于点I，在△MHN中，根据平行线分线段成比例即可证明MI=IN．
| PG |
| PB |
| PE |
| PH |
| PG |
| PB |
| PF |
| PN |
| PE |
| PH |
| PF |
| PN |
解答：
证明：取BD中点G，连结EG、FG，延长ME到H，使HE=ME，连结HB、HN．
∵E是AB中点，G是BD中点，
∴EG∥AD，同理GF∥BC．
易证△BEH≌△AEM（SAS），
∴∠BHE=∠AME，
∴BH∥AM，
∵EG∥AM，
∴EG∥BH，
∴
=
，
∵GF∥BN，
∴
=
，
∴
=
，
∴EF∥HN．
设直线EF与MN交于点I，
在△MHN中，∵EI∥HN，HE=ME，
∴
=
=1，
∴MI=IN，
即直线EF平分MN．
证明：取BD中点G，连结EG、FG，延长ME到H，使HE=ME，连结HB、HN．∵E是AB中点，G是BD中点，
∴EG∥AD，同理GF∥BC．
易证△BEH≌△AEM（SAS），
∴∠BHE=∠AME，
∴BH∥AM，
∵EG∥AM，
∴EG∥BH，
∴
| PG |
| PB |
| PE |
| PH |
∵GF∥BN，
∴
| PG |
| PB |
| PF |
| PN |
∴
| PE |
| PH |
| PF |
| PN |
∴EF∥HN．
设直线EF与MN交于点I，
在△MHN中，∵EI∥HN，HE=ME，
∴
| MI |
| IN |
| ME |
| EH |
∴MI=IN，
即直线EF平分MN．
点评：本题考查了平行线分线段成比例定理，三角形中位线定理，全等三角形的判定与性质，平行线的判定，有一定难度．准确作出辅助线是解题的关键．
练习册系列答案
相关题目
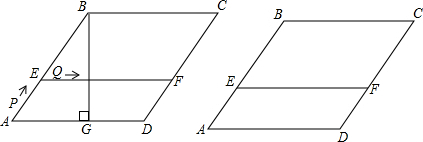
如图所示，已知AB⊥BC，DC⊥BC，E在BC上，且AE=AD，AB=BC，求证：CE=CD．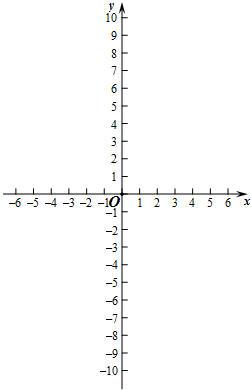
在平面直角坐标系xOy中，抛物线y=x2-（m-1）x-m（m＞0）与x轴交于A，B两点（点A在点B的左侧），与y轴交于点C．
如图所示，△ABC为等边三角形，D、E分别是AC、BC上的点，且AD=CE，AE与BD相交于点P，BF⊥AE于F，求证：BP=2PF．
如图，AB是⊙O的直径，且AD∥OC，若弧AD的度数为80°，求弧CD的度数．
如图，在直角坐标系中，边长为2的等边△ABC，顶点A在l：y=-x+4上滑动，边BC保持水平状态，当点C刚好落在坐标轴上时，求点B的坐标．