题目内容
已知三点(0,4)、(t,9)、(-2,-4)在同一条直线上,则t= .
考点:一次函数图象上点的坐标特征
专题:
分析:设这条直线解析式为y=kx+b,先把(0,4)、(-2,-4)点坐标代入得到k和b的方程组,解方程组求出k和b的值,得到直线解析式,然后把(t,9)代入此解析式得到t的一元一次方程,然后解一元一次方程即可.
解答:解:设这条直线解析式为y=kx+b,把(0,4)、(-2,-4)点坐标代入得
,
解得:
,
所以直线解析式为y=4x+4,
把(t,9)代入此解析式得4t+4=9,
解得:t=
.
故答案为:
.
|
解得:
|
所以直线解析式为y=4x+4,
把(t,9)代入此解析式得4t+4=9,
解得:t=
| 5 |
| 4 |
故答案为:
| 5 |
| 4 |
点评:本题考查了待定系数法求一次函数解析式:(1)先设出函数的一般形式,如求一次函数的解析式时,先设y=kx+b;(2)将自变量x的值及与它对应的函数值y的值代入所设的解析式,得到关于待定系数的方程或方程组;(3)解方程或方程组,求出待定系数的值,进而写出函数解析式.也考查了一次函数图象上点的坐标特征.

练习册系列答案
相关题目
在半径为10的⊙O中,弦AB=12,弦CD=16,且AB∥CD,则弦AB、CD的距离为( )
| A、14 | B、2 |
| C、8或6 | D、14或2 |
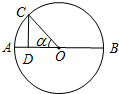 如图,AB为⊙O的直径,D为AB上一点,且AB=6AD,CD⊥AB于D,C在⊙O上,设∠COD=α,则tan
如图,AB为⊙O的直径,D为AB上一点,且AB=6AD,CD⊥AB于D,C在⊙O上,设∠COD=α,则tan| α |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
李华把向东移动记作“+”,向西移动记作“-”,下列说法不正确的是( )
| A、-5米表示向西移动了5米 |
| B、+5米表示向东移动了5米 |
| C、向东移动-5米表示向西移动-5米 |
| D、向西移动5米,也可记作向东移动-5米 |
已知点A(-3,y1),B(-1,y2),C(2,y3)在抛物线y=
x2上,则y1,y2,y3的大小关系是( )
| 2 |
| 3 |
| A、y1<y2<y3 |
| B、y1>y2>y3 |
| C、y1<y3<y2 |
| D、y2<y3<y1 |
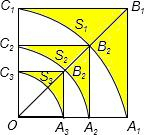 如图,正方形OA1B1C1的边长为2,以O为圆心,OA1为半径作弧A1C1交OB1于点B2,设弧A1C1与边A1B1,B1C1围成的阴影部分的面积为S1.然后以OB2为对角线作正方形OA2B2C2,又以O为圆心、OA2为半径作弧A2C2交OB2于点B3,设弧A2C2与边A2B2、B2C2围成的阴影部分的面积为S2,…,按此规律继续作下去,设弧AnCn,BnCn围成的阴影部分的面积为Sn,设S=S1+S2+S2+…+Sn,则S=
如图,正方形OA1B1C1的边长为2,以O为圆心,OA1为半径作弧A1C1交OB1于点B2,设弧A1C1与边A1B1,B1C1围成的阴影部分的面积为S1.然后以OB2为对角线作正方形OA2B2C2,又以O为圆心、OA2为半径作弧A2C2交OB2于点B3,设弧A2C2与边A2B2、B2C2围成的阴影部分的面积为S2,…,按此规律继续作下去,设弧AnCn,BnCn围成的阴影部分的面积为Sn,设S=S1+S2+S2+…+Sn,则S= 某学校九年级的小红同学,在自己家附近进行测量一座楼房高度的实践活动,如图,她在山坡脚A处测得这座楼房顶B点的仰角为60°,沿山坡向上走到C处再测得B点的仰角为45°,已知OA=200m,山坡的坡度i=
某学校九年级的小红同学,在自己家附近进行测量一座楼房高度的实践活动,如图,她在山坡脚A处测得这座楼房顶B点的仰角为60°,沿山坡向上走到C处再测得B点的仰角为45°,已知OA=200m,山坡的坡度i=