题目内容
2.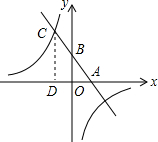 已知,如图,一次函数y=kx+b(k、b为常数,k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数xy=n(n为常数且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂直为D.若OB=2OA=3OD=6.则反比例函数的解析式为y=-$\frac{20}{x}$.
已知,如图,一次函数y=kx+b(k、b为常数,k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数xy=n(n为常数且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂直为D.若OB=2OA=3OD=6.则反比例函数的解析式为y=-$\frac{20}{x}$.
分析 证出DC∥OB,得出比例式求出CD=10,得出点C的坐标,即可求出反比例函数解析式.
解答 解:∵OB=2OA=3OD=6,
∴OB=6,OA=3,OD=2,
∵CD⊥OA,
∴DC∥OB,
∴$\frac{OB}{CD}=\frac{AO}{AD}$,
∴$\frac{6}{CD}=\frac{3}{5}$,
∴CD=10,
∴点C坐标(-2,10),
∵反比例函数xy=n经过点C(-2,10),
∴n=-20,
∴反比例函数解析式为y=-$\frac{20}{x}$;
故答案为:y=-$\frac{20}{x}$.
点评 本题考查一次函数与反比例函数的交点问题、平行线分线段成比例定理,求出点C的坐标是解决问题的关键.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
11.甲、乙两名运动员在某项射击比赛中10次射击的平均成绩都是7环,而甲、乙的成绩的方差分别为1.21和3.12,由此可知( )
| A. | 甲比乙的成绩稳定 | B. | 乙比甲的成绩稳定 | ||
| C. | 甲、乙的成绩一样稳定 | D. | 无法确定谁的成绩更稳定 |
 如图是由一些小正方体组合而成的几何体的俯视图,小正方形中的数字表示该位置小正方体的个数,则这个几何体主视图是( )
如图是由一些小正方体组合而成的几何体的俯视图,小正方形中的数字表示该位置小正方体的个数,则这个几何体主视图是( )



 在下面过程中的横线上填空,并在括号内注明理由.
在下面过程中的横线上填空,并在括号内注明理由.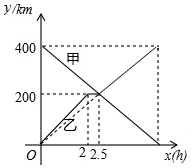 甲,乙两辆汽车分别从A,B两地同时出发,沿同一条公路相向而行,已知甲车匀速行驶;乙车出发2h后休息,与甲车相遇后继续行驶,结果同时分别到达B,A两地.设甲、乙两车与B地的距离分别为y甲(km),y乙(km
甲,乙两辆汽车分别从A,B两地同时出发,沿同一条公路相向而行,已知甲车匀速行驶;乙车出发2h后休息,与甲车相遇后继续行驶,结果同时分别到达B,A两地.设甲、乙两车与B地的距离分别为y甲(km),y乙(km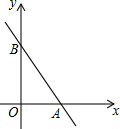 如图,直线y=kx+b与坐标轴交于A(3,0),B(0,5)两点,则不等式kx+b≤0的解集为x≥3.
如图,直线y=kx+b与坐标轴交于A(3,0),B(0,5)两点,则不等式kx+b≤0的解集为x≥3.