题目内容
17. 甲,乙两辆汽车分别从A,B两地同时出发,沿同一条公路相向而行,已知甲车匀速行驶;乙车出发2h后休息,与甲车相遇后继续行驶,结果同时分别到达B,A两地.设甲、乙两车与B地的距离分别为y甲(km),y乙(km
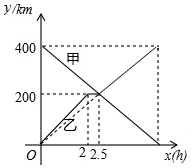
甲,乙两辆汽车分别从A,B两地同时出发,沿同一条公路相向而行,已知甲车匀速行驶;乙车出发2h后休息,与甲车相遇后继续行驶,结果同时分别到达B,A两地.设甲、乙两车与B地的距离分别为y甲(km),y乙(km),甲车行驶的时间为x(h),y甲,y乙与x之间的函数图象如图所示,结合图象解答下列问题:
(1)当0<x<2时,求乙车的速度;
(2)求乙车与甲车相遇后y乙与x的关系式;
(3)当两车相距20km时,直接写出x的值.
分析 (1)根据速度=路程÷时间,即可求出当0<x<2时,乙车的速度;
(2)根据速度=路程÷时间可求出甲车的速度,由时间=路程÷速度可求出甲、乙两车到达目的地的时间,再结合二者相遇的时间,利用待定系数法即可求出乙车与甲车相遇后y乙与x的关系式;
(3)根据数量关系,找出y甲、y乙关于x的函数关系式,分0≤x<2、2≤x<2.5和2.5≤x≤5三种情况,找出关于x的一元一次方程,解之即可得出结论.
解答 解:(1)200÷2=100(km/h).
答:当0<x<2时,乙车的速度为100km/h.
(2)甲车的速度为(400-200)÷2.5=80(km/h),
甲、乙两车到达目的地的时间为400÷80=5(h).
设乙车与甲车相遇后y乙与x的关系式为y乙=kx+b,
将点(2.5,200)、(5,400)代入y乙=kx+b,
$\left\{\begin{array}{l}{2.5k+b=200}\\{5k+b=400}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=80}\\{b=0}\end{array}\right.$,
∴乙车与甲车相遇后y乙与x的关系式为y乙=80x(2.5≤x≤5).
(3)根据题意得:y乙=$\left\{\begin{array}{l}{100x(0≤x<2)}\\{200(2≤x<2.5)}\\{80x(2.5≤x≤5)}\end{array}\right.$,
y甲=400-80x(0≤x≤5).
当0≤x<2时,400-80x-100x=20,
解得:x=$\frac{19}{9}$>2(不合题意,舍去);
当2≤x<2.5时,400-80x-200=20,
解得:x=$\frac{9}{4}$;
当2.5≤x≤5时,80x-(400-80x)=20,
解得:x=$\frac{21}{8}$.
综上所述:当x的值为$\frac{9}{4}$或$\frac{21}{8}$时,两车相距20km.
点评 本题考查了一次函数的应用、待定系数法求一次函数解析式以及解一元一次方程,解题的关键是:(1)根据数量关系,列式计算;(2)根据点的坐标,利用待定系数法求出一次函数关系式;(3)分0≤x<2、2≤x<2.5和2.5≤x≤5三种情况,找出关于x的一元一次方程.

| A. | 扩大6倍 | B. | 不变 | C. | 扩大3倍 | D. | 缩小3倍 |
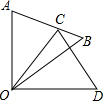 如图,△COD是△AOB绕点O顺时针方向旋转38°后所得的图形,点C恰好在AB上,∠AOD=90°,那么∠BOC的度数为( )
如图,△COD是△AOB绕点O顺时针方向旋转38°后所得的图形,点C恰好在AB上,∠AOD=90°,那么∠BOC的度数为( )| A. | 12° | B. | 14° | C. | 24° | D. | 30° |
| A. | 30°,75° | B. | 40°,95° | C. | 50°,115° | D. | 55°,125° |
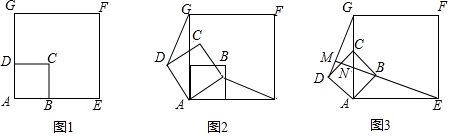
 如图,在?ABCD中,∠B=60°,点E、F分别是边BC、AB上的点,且DF垂直平分AE,若BF=1,且EF⊥AB,则线段AD的长为$\sqrt{3}+$3.
如图,在?ABCD中,∠B=60°,点E、F分别是边BC、AB上的点,且DF垂直平分AE,若BF=1,且EF⊥AB,则线段AD的长为$\sqrt{3}+$3.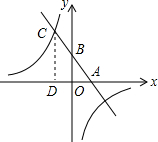 已知,如图,一次函数y=kx+b(k、b为常数,k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数xy=n(n为常数且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂直为D.若OB=2OA=3OD=6.则反比例函数的解析式为y=-$\frac{20}{x}$.
已知,如图,一次函数y=kx+b(k、b为常数,k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数xy=n(n为常数且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂直为D.若OB=2OA=3OD=6.则反比例函数的解析式为y=-$\frac{20}{x}$. 如图,一段抛物线:y=-x(x-3)(0≤x≤3),记为C1,它与x轴交于点O,A1;将C1绕点A2旋转180°得C2,交x轴于点A2;将C2绕点A2旋转180°得C3,交x轴于点A3;…,如此进行下去,直至得C13,若P(38,m)在第13段抛物线C13上,则m=2.
如图,一段抛物线:y=-x(x-3)(0≤x≤3),记为C1,它与x轴交于点O,A1;将C1绕点A2旋转180°得C2,交x轴于点A2;将C2绕点A2旋转180°得C3,交x轴于点A3;…,如此进行下去,直至得C13,若P(38,m)在第13段抛物线C13上,则m=2.