Question

1．如图，正方形网格中的每个小正方形的边长都是1，每个小方格的顶点叫做格点．
（1）以格点为顶点画△ABC，使得AB=$\sqrt{5}$，BC=$\frac{5}{9}\sqrt{81}$，AC=$\frac{\sqrt{40}}{\sqrt{2}}$（先化简，再作图）
（2）求△ABC的面积．

Answer 1

分析 （1）每个小正方形的边长均为1，利用勾股定理得出AB=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$，BC=5=$\sqrt{{3}^{2}+{4}^{2}}$，AC=$\frac{\sqrt{40}}{\sqrt{2}}$=$\sqrt{{2}^{2}+{4}^{2}}$，据此画出三角形；
（2）利用三角形的面积=矩形的面积-3个小直角三角形的面积进行解答．

解答 解：（1）BC=$\frac{5}{9}\sqrt{81}$=5，AC=$\frac{\sqrt{40}}{\sqrt{2}}$=2$\sqrt{5}$．
∵AB=$\sqrt{{1}^{2}+{2}^{2}}$，BC=5=$\sqrt{{3}^{2}+{4}^{2}}$，
∴画△ABC如图所示：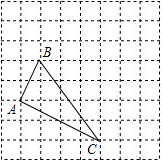
；

（2）△ABC的面积=5×4-$\frac{1}{2}$×2×4-$\frac{1}{2}$×3×4-$\frac{1}{2}$×1×2=9，即△ABC的面积是9．

点评 本题考查了勾股定理、直角三角形的面积．在解答（2）题时，利用了“分割法”来求△ABC的面积．