题目内容
14. 如图,AB为⊙O的直径,C为⊙O上一点,弦AD平分∠BAC,交BC于点E,AB=6,AD=5,则DE的长为( )
如图,AB为⊙O的直径,C为⊙O上一点,弦AD平分∠BAC,交BC于点E,AB=6,AD=5,则DE的长为( )| A. | 2.2 | B. | 2.5 | C. | 2 | D. | 1.8 |
分析 连接BD、CD,由勾股定理先求出BD的长,再利用△ABD∽△BED,得出$\frac{DE}{DB}$=$\frac{DB}{AD}$,可解得DE的长.
解答 解:如图1,连接BD、CD,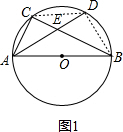 ,
,
∵AB为⊙O的直径,
∴∠ADB=90°,
∴BD=$\sqrt{A{B}^{2}-A{D}^{2}}$=$\sqrt{{6}^{2}-{5}^{2}}$=$\sqrt{11}$,
∵弦AD平分∠BAC,
∴CD=BD=$\sqrt{11}$,
∴∠CBD=∠DAB,
在△ABD和△BED中,
$\left\{\begin{array}{l}{∠BAD=∠EBD}\\{∠ADB=∠BDE}\end{array}\right.$
∴△ABD∽△BED,
∴$\frac{DE}{DB}=\frac{DB}{AD}$,即$\frac{DE}{\sqrt{11}}=\frac{\sqrt{11}}{5}$,
解得DE=$\frac{11}{5}$.
故选A.
点评 此题主要考查了三角形相似的判定和性质及圆周角定理,解答此题的关键是得出△ABD∽△BED.

练习册系列答案
 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案 小学学习好帮手系列答案
小学学习好帮手系列答案
相关题目
 已知平行四边形ABCD,AC与BD交于O点,EF过点O且EF⊥AB,AC=$\sqrt{5}$EF,∠ACB=45°.
已知平行四边形ABCD,AC与BD交于O点,EF过点O且EF⊥AB,AC=$\sqrt{5}$EF,∠ACB=45°.
 已知,Rt△ABC中,∠ACB=90°,AC=BC,∠ABC的角平分线交AC于E,AD⊥BE于D,求证:AD=$\frac{1}{2}$BE.
已知,Rt△ABC中,∠ACB=90°,AC=BC,∠ABC的角平分线交AC于E,AD⊥BE于D,求证:AD=$\frac{1}{2}$BE. 如图,双曲线y=$\frac{3}{x}$与直线y=$\frac{2}{3}$x+1交于A、B两点,A点在B点的右侧.
如图,双曲线y=$\frac{3}{x}$与直线y=$\frac{2}{3}$x+1交于A、B两点,A点在B点的右侧.